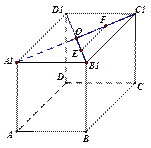
题目内容
对于平面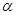 和直线
和直线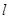 ,
,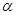 内至少有一条直线与直线
内至少有一条直线与直线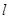 ( )
( )
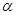 和直线
和直线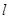 ,
,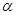 内至少有一条直线与直线
内至少有一条直线与直线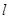 ( )
( )| A.平行 | B.垂直 | C.异面 | D.相交 |
B
若 ,则
,则 内存在至少一条直线与直线
内存在至少一条直线与直线 平行,垂直或相交,但不可能异面,C排除;若
平行,垂直或相交,但不可能异面,C排除;若 ,则
,则 内存在至少一条直线与直线
内存在至少一条直线与直线 平行或垂直,不可能相交,D排除;若
平行或垂直,不可能相交,D排除;若 ,则
,则 内存在至少一条直线与直线
内存在至少一条直线与直线 垂直,不可能平行,A排除。所以选B
垂直,不可能平行,A排除。所以选B
 ,则
,则 内存在至少一条直线与直线
内存在至少一条直线与直线 平行,垂直或相交,但不可能异面,C排除;若
平行,垂直或相交,但不可能异面,C排除;若 ,则
,则 内存在至少一条直线与直线
内存在至少一条直线与直线 平行或垂直,不可能相交,D排除;若
平行或垂直,不可能相交,D排除;若 ,则
,则 内存在至少一条直线与直线
内存在至少一条直线与直线 垂直,不可能平行,A排除。所以选B
垂直,不可能平行,A排除。所以选B
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 为平行四边形,
为平行四边形,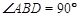 ,
,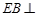 平面
平面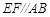 ,
,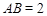 ,
, ,
,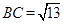 ,且
,且 是
是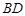 的中点.
的中点. 平面
平面 ;
;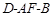 的大小;
的大小;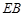 上是否存在一点
上是否存在一点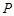 ,使得
,使得 与
与 所成的角为
所成的角为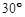 ? 若存在,求出
? 若存在,求出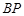 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.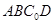 中,
中,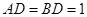 ,
,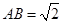 。沿它的对角线
。沿它的对角线 把△
把△ 折起,使点
折起,使点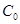 到达平面
到达平面 的位置。
的位置。 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角 的大小。
的大小。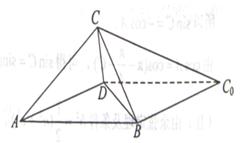
 ,
, ,直线
,直线 ,若
,若 ,则
,则  的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.
 所在的平面垂直于矩形
所在的平面垂直于矩形 所在的平面,
所在的平面,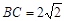 ,
,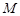 为
为 的中点.
的中点.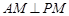 ;
;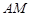 和
和 所成角的余弦值.
所成角的余弦值.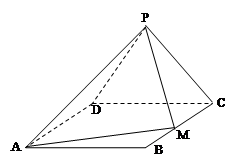
 中,底面
中,底面 是菱形,
是菱形, .
. ,求证:
,求证: 平面
平面 ;
; 平
平 面
面 ;
; 上是否存在点
上是否存在点 (异于点
(异于点 )使得
)使得 ∥平面
∥平面 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 中,底面
中,底面 为正方形,侧棱
为正方形,侧棱 底面
底面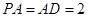 ,点
,点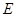 为
为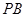 的中点。
的中点。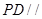 平面
平面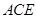 ;
;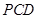 的距离。
的距离。
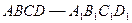 中,
中,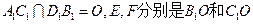 的中点,则在长方体各棱中与EF平行的有( )
的中点,则在长方体各棱中与EF平行的有( )