题目内容
如图，在梯形ABCD中，AD//BC，AC、BD相交于O，记△BCO、△CDO、△ADO的面积分别为S1、S2、S3，则
的取值范围是 .
【
】
解析考点：平行线等分线段定理．
分析：根据三角形相似的引理，我们易判断△AOD∽△COB，然后根据三角形相似的性质得到对应边成比例，而根据同高的两个三角形面积之比等于底边长之比，结合基本不等式即可求出的取值范围．
解：∵AD∥BC，
∴△AOD∽△COB
∴
=
∴=
+
=
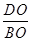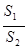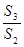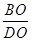+≥2
=2
当且仅当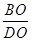=时，即BO=DO时，即O为BD中点时取等；
又∵四边形ABCD为梯形，故O不可能为BD的中点，
故＞2
即的取值范围（2，+∞）
故答案为：（2，+∞）
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
，AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论：
，给出空间中三棱锥的有关结论：________
能被3整除” 的第二步中,当
时,为了使用归纳假设,应将
变形为 
若
均为实数），
时，由
的假设到证明
时，等式左边应添加的式子是 ．
，
，
，
，
，可以得出的一般结论是 
，在验证当n=1时,等式