题目内容
11.(理)函数$f(x)=\frac{9}{{{x^2}+1}}+\frac{4}{{4-{x^2}}}$(-2<x<2)的最小值为5.分析 运用乘1法,可得f(x)=$\frac{1}{5}$•5($\frac{9}{1+{x}^{2}}$+$\frac{4}{4-{x}^{2}}$)=$\frac{1}{5}$[(1+x2)+(4-x2)]($\frac{9}{1+{x}^{2}}$+$\frac{4}{4-{x}^{2}}$),展开后再用基本不等式,即可得到所求最小值.
解答 解:f(x)=$\frac{1}{5}$•5($\frac{9}{1+{x}^{2}}$+$\frac{4}{4-{x}^{2}}$)
=$\frac{1}{5}$[(1+x2)+(4-x2)]($\frac{9}{1+{x}^{2}}$+$\frac{4}{4-{x}^{2}}$)
=$\frac{1}{5}$[13+$\frac{9(4-{x}^{2})}{1+{x}^{2}}$+$\frac{4(1+{x}^{2})}{4-{x}^{2}}$]
≥$\frac{1}{5}$(13+2$\sqrt{9•4}$)=5.
当且仅当2(1+x2)=3(4-x2),即x=±$\sqrt{2}$时,
f(x)取得最小值5.
故答案为:5.
点评 本题考查函数的最值的求法,注意运用乘1法和基本不等式,考查运算能力,属于中档题和易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.经过直线$l:x+y-2\sqrt{2}=0$上的点P,向圆O:x2+y2=1引切线,切点为A,则切线长|PA|的最小值为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
6.已知数列{an},满足a1=1,an-an-1=n,则a10=( )
| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
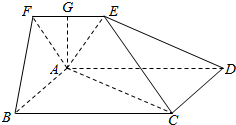 如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,G是EF的中点,AG=1
如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,G是EF的中点,AG=1