题目内容

在平面直角坐标系中，若定点A（1，2）与动点P（x，y）满足向量 $数学公式$ 在向量 $数学公式$ 上的投影为 $数学公式$ ，则点P的轨迹方程是

A.
x-2y+5=0
B.
x+2y-5=0
C.
x+2y+5=0
D.
x-2y-5=0

C
分析：根据向量 $\text{[math]}$ 在向量 $\text{[math]}$ 上的投影为 $\text{[math]}$ ，可得关系x，y的一方程，化简即为所求轨迹方程．
解答：由于定点A（1，2）与动点P（x，y）满足向量 $\text{[math]}$ 在向量 $\text{[math]}$ 上的投影为 $\text{[math]}$ ，
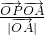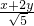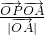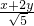根据向量投影定义得， $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，即x+2y+5=0，
∴点P的轨迹方程是x+2y+5=0，
故选C．
点评：本题考查轨迹方程的求法及向量投影的定义，本题中轨迹方程的求解采取直接法，理解向量投影定义是解决本题的关键．

练习册系列答案

新编单元测试AB卷系列答案

期末夺冠满分测评卷系列答案

创新考王完全试卷系列答案

期末复习检测系列答案

超能学典单元期中期末专题冲刺100分系列答案

期末100分冲刺卷系列答案

黄冈360度定制密卷系列答案

聚能闯关期末复习冲刺卷系列答案

同步测试卷过关冲刺100分系列答案

阳光考场单元测试卷系列答案

相关题目

在平面直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为：pcos(θ-

)=1，M，N分别为曲线C与x轴，y轴的交点，则MN的中点P在平面直角坐标系中的坐标为

在平面直角坐标系中，A（3，0）、B（0，3）、C（cosθ，sinθ），θ∈(

|．
（1）求角θ的值；
（2）设α＞0，0＜β＜

θ，求y=2-sin²α-cos²β的最小值．

在平面直角坐标系中，如果x与y都是整数，就称点（x，y）为整点，下列命题中正确的是

（写出所有正确命题的编号）．
①存在这样的直线，既不与坐标轴平行又不经过任何整点
②如果k与b都是无理数，则直线y=kx+b不经过任何整点
③直线l经过无穷多个整点，当且仅当l经过两个不同的整点
④直线y=kx+b经过无穷多个整点的充分必要条件是：k与b都是有理数
⑤存在恰经过一个整点的直线．

在平面直角坐标系中，下列函数图象关于原点对称的是（　　）

在平面直角坐标系中，以点（1，0）为圆心，r为半径作圆，依次与抛物线y²=x交于A、B、C、D四点，若AC与BD的交点F恰好为抛物线的焦点，则r=