题目内容
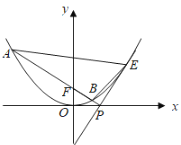
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 参数方程为
参数方程为![]() 为参数),将曲线
为参数),将曲线![]() 上所有点的横坐标变为原来的
上所有点的横坐标变为原来的![]() ,纵坐标变为原来的
,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 取得最小值时
取得最小值时![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]()
【解析】
(1)利用![]() 消去参数
消去参数![]() ,求得曲线
,求得曲线![]() 的直角坐标方程.根据坐标变换的知识求得
的直角坐标方程.根据坐标变换的知识求得![]() 的普通方程.
的普通方程.
(2)设出直线![]() 的参数方程,代入
的参数方程,代入![]() 的方程并写出根与系数关系,求得弦长
的方程并写出根与系数关系,求得弦长![]() 的表达式,并利用三角函数最值的求法求得
的表达式,并利用三角函数最值的求法求得![]() 取得最小值时
取得最小值时![]() 的值.
的值.
(1)将曲线![]() 参数方程
参数方程![]() 为参数)的参数消去,得到直角坐标方程为
为参数)的参数消去,得到直角坐标方程为![]() ,设
,设![]() 上任意一点为
上任意一点为![]() ,经过伸缩变换后的坐标为
,经过伸缩变换后的坐标为![]() ,由题意得:
,由题意得:
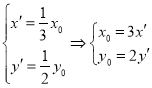 ,故
,故![]() ;
;
(2)过点![]() 倾斜角为
倾斜角为![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() 为参数),带入
为参数),带入![]() 的方程
的方程![]() 得:
得:![]() ,
,
记![]() 对于的参数分别为
对于的参数分别为![]() ,
,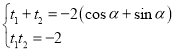 ,
,
![]() ,
,
故当![]() 时,
时,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目