题目内容
6.已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.(1)求数列{an}的通项公式;
(2)若bn=anlog${\;}_{\frac{1}{2}}$an,Sn=b1+b2+b3+…+bn,求Sn;
(3)在(2)的条件下,若对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
分析 (1)通过a3+2是a2,a4的等差中项可知2(a3+2)=a2+a4,结合a2+a3+a4=28可知a3=8,进而通过解方程$\frac{8}{q}$+8q=20可知公比q=2,计算即得结论;
(2)通过(1)可知bn=-n•2n,利用错位相减法计算即得结论;
(3)通过(2)并整理可知,对任意正整数n,Sn+(n+m)an+1<0恒成立等价于m<$\frac{1}{{2}^{n}}$-1对任意正整数n恒成立,问题转化为求f(n)=$\frac{1}{{2}^{n}}$-1的最小值,计算即得结论.
解答 解:(1)∵a3+2是a2,a4的等差中项,
∴2(a3+2)=a2+a4,
又∵a2+a3+a4=28,
∴2(a3+2)=28-a3,
解得:a3=8,
∴a2+a4=20,
设等比数列{an}的公比为q,则$\frac{8}{q}$+8q=20,
解得:q=2或q=$\frac{1}{2}$(舍),
∴数列{an}的通项公式an=2n;
(2)由(1)可知bn=anlog${\;}_{\frac{1}{2}}$an=-n•2n,
∴-Sn=-(b1+b2+b3+…+bn)=1•2+2•22+…+n•2n,
则-2Sn=1•22+2•23+…+(n-1)•2n+n•2n+1,
两式相减得:Sn=2+22+23+…+2n-n•2n+1
=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1
=-2+2n+1-n•2n+1,
∴Sn=-2+(1-n)•2n+1;
(3)由(2)可知,对任意正整数n,Sn+(n+m)an+1<0恒成立,
即-2+(1-n)•2n+1+(n+m)an+1<0恒成立,
整理得:m<$\frac{1}{{2}^{n}}$-1对任意正整数n恒成立,
易知f(n)=$\frac{1}{{2}^{n}}$-1随着n的增大而减小,即f(n)∈(-1,-$\frac{1}{2}$],
∴m≤-1.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{9}$ |
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 合计 | 26 | 24 | 50 |
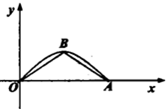 如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )
如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm),若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118)内该厂可获利分别为10,30,20,10(单位:元),现在该厂生产的产品中随机抽取200件测量它们的直径,得到如图所示的频率直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm),若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118)内该厂可获利分别为10,30,20,10(单位:元),现在该厂生产的产品中随机抽取200件测量它们的直径,得到如图所示的频率直方图.