题目内容
14.函数f(x)=lg(4-x)+x0的定义域是{x|x<4,且x≠0}.分析 容易看出该函数有意义时,x满足$\left\{\begin{array}{l}{4-x>0}\\{x≠0}\end{array}\right.$,解该不等式组即可得出函数f(x)的定义域.
解答 解:要使原函数有意义,则:
$\left\{\begin{array}{l}{4-x>0}\\{x≠0}\end{array}\right.$;
∴x<4,且x≠0;
∴函数f(x)的定义域为{x|x<4,且x≠0}.
故答案为:{x|x<4,且x≠0}.
点评 考查函数定义域的概念及求法,对数的真数大于0,对于x0,x≠0.

练习册系列答案
相关题目
5.过曲线y=xex上横坐标为1的点的切线方程为( )
| A. | 2ex-y-e=0 | B. | ex-y=0 | C. | x-y+1=0 | D. | x-y-1=0 |
4.三个数50.6,0.65,log0.65的大小顺序是( )
| A. | 0.65<log0.65<50.6 | B. | 0.65<50.6<log0.65 | ||
| C. | log0.65<0.65<50.6 | D. | log0.65<50.6<0.65 |
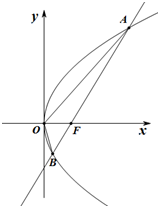 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1),B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1),B(x2,y2)两点,且y1y2=-4. 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$. 如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.
如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.