题目内容
设实数
满足
，则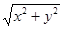
的最大值是_____.
2.
解析试题分析：由题意，
，即
，因此只要求出
的最大值即可，又由得
，∴
，即最大值为2，故
的最大值为
.
考点：约束条件下的最值问题.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
轻松夺冠全能掌控卷系列答案题目内容
设实数满足，则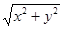的最大值是_____.
2.
解析试题分析：由题意，，即，因此只要求出的最大值即可，又由得，∴，即最大值为2，故的最大值为.
考点：约束条件下的最值问题.
轻松夺冠全能掌控卷系列答案
，在
上单调递减，则a的取值范围是 .
,若其定义域内存在两个实数
，使得
时，
的值域也是
,则称函数
是“和谐函数”，则实数
的取值范围是 ．
，则
= .
对于
，
恒成立，则实数
的取值范围是___________.
是
上的奇函数,且
对称,当
时,
，则
.
的值域是____________.
定义在R上的奇函数，当
时，
，给出下列命题：
时，
②函数
的解集为
④
，都有
满足条件
，且
，则
.