题目内容
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求乙获胜且比赛局数多于5局的概率;
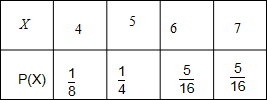
(2)求比赛局数X的分布列和数学期望E(X).
(1)求乙获胜且比赛局数多于5局的概率;
(2)求比赛局数X的分布列和数学期望E(X).
分析:(1)乙获胜且比赛局数多于5局,分为乙获胜需要打6局或7局,根据二项分布的概率计算公式及相互独立事件的概率计算公式及互斥事件的概率计算公式即可.
(2)利用二项分布、相互独立事件的概率计算公式及互斥事件的概率计算公式即可.
(2)利用二项分布、相互独立事件的概率计算公式及互斥事件的概率计算公式即可.
解答:解:(1)∵两人在每一局比赛中获胜的可能性相同,∴P(甲)=P(乙)=
.
∵乙获胜且比赛局数多于5局,∴乙获胜需要打6局或7局.
①乙获胜需要打6局时,乙在前5局中只赢了3局,其概率P6=
(
)3(
)2×
=
;
②乙获胜需要打7局时,乙在前6局中只赢了3局,其概率P7=
(
)3(
)3×
=
.
根据互斥事件的概率计算公式乙获胜且比赛局数多于5局的概率=P6+P7=
+
=
;
(2)P(X=4)=(
)4+(
)4=
;
P(X=5)=2
(
)3×
×
=
;
P(X=6)=2P6=2×
=
;
P(X=7)=2P7=2×
=
.
其分步列如下表:
∴E(X)=4×
+5×
+6×
+7×
=
.
| 1 |
| 2 |
∵乙获胜且比赛局数多于5局,∴乙获胜需要打6局或7局.
①乙获胜需要打6局时,乙在前5局中只赢了3局,其概率P6=
| C | 3 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 26 |

②乙获胜需要打7局时,乙在前6局中只赢了3局,其概率P7=
| C | 3 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 20 |
| 27 |
根据互斥事件的概率计算公式乙获胜且比赛局数多于5局的概率=P6+P7=
| 10 |
| 26 |
| 20 |
| 27 |
| 5 |
| 16 |
(2)P(X=4)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 23 |
P(X=5)=2
| C | 3 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
P(X=6)=2P6=2×
| 10 |
| 26 |
| 5 |
| 24 |
P(X=7)=2P7=2×
| 20 |
| 27 |
| 5 |
| 24 |
其分步列如下表:
∴E(X)=4×
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 93 |
| 16 |
点评:熟练掌握二项分布的概率计算公式、相互独立事件的概率计算公式及互斥事件的概率计算公式是解题的关键.

练习册系列答案
相关题目
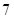 局
局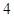 胜制(即先胜
胜制(即先胜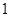 获胜的概率;
获胜的概率; 局的概率;
局的概率;