题目内容
设函数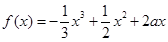 ,
,
(1)若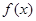 在
在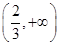 上存在单调增区间,求实数
上存在单调增区间,求实数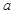 的取值范围;
的取值范围;
(2)当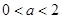 时
时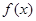 在
在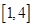 上的最小值为
上的最小值为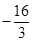 ,求
,求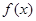 在该区间上的最大值.
在该区间上的最大值.
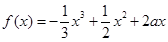 ,
,(1)若
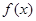 在
在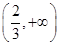 上存在单调增区间,求实数
上存在单调增区间,求实数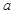 的取值范围;
的取值范围;(2)当
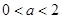 时
时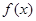 在
在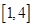 上的最小值为
上的最小值为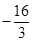 ,求
,求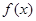 在该区间上的最大值.
在该区间上的最大值.(1)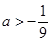
(2)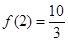
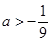
(2)
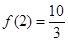
解:(1)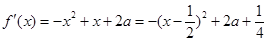
其对称轴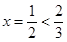 在
在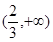 上
上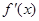 递减
递减
要使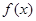 在
在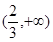 上存在单调增区间,只须
上存在单调增区间,只须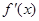 在
在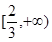 上的最大值
上的最大值
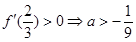
∴当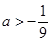 时,
时,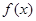 在
在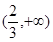 上存在单调增区间。
上存在单调增区间。
(2)由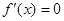 得
得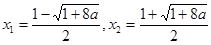
∵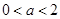 ∴
∴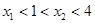
在[1,4]上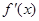 的图象与x轴的交点只有一个
的图象与x轴的交点只有一个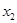
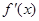 ,
,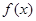 在[1,4]上随x变化如下表:
在[1,4]上随x变化如下表:
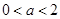
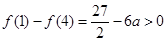
故在[1,4]上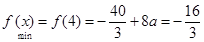
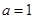
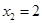
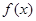 的最大值
的最大值 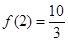
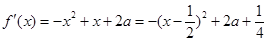
其对称轴
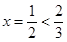 在
在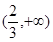 上
上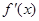 递减
递减要使
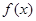 在
在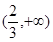 上存在单调增区间,只须
上存在单调增区间,只须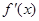 在
在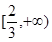 上的最大值
上的最大值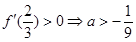
∴当
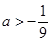 时,
时,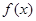 在
在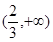 上存在单调增区间。
上存在单调增区间。(2)由
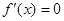 得
得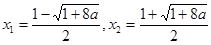
∵
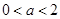 ∴
∴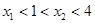
在[1,4]上
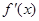 的图象与x轴的交点只有一个
的图象与x轴的交点只有一个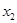
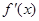 ,
,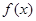 在[1,4]上随x变化如下表:
在[1,4]上随x变化如下表:| x | 1 | 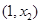 | 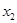 |  | 4 |
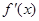 | | + | 0 | — | |
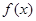 | 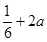 | ↗ | 最大值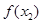 | ↘ | 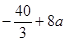 |
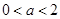
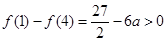
故在[1,4]上
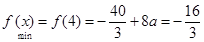
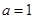
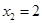
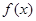 的最大值
的最大值 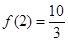

练习册系列答案
相关题目
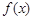 的定义域为开区间
的定义域为开区间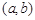 ,导函数
,导函数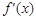 在
在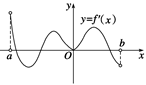
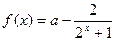 ,
,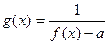
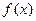 为奇函数,求
为奇函数,求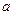 的值。
的值。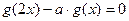 ,有唯一实数解,求
,有唯一实数解,求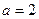 ,则是否存在实数
,则是否存在实数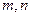 (
(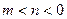 ),使得函数
),使得函数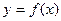 的定义域和值域都为
的定义域和值域都为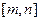 。若存在,求出
。若存在,求出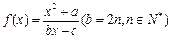 的定义域为{x| x ≠1},图象过原点,且
的定义域为{x| x ≠1},图象过原点,且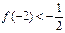 .
.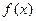 的单调减区间;
的单调减区间;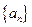 前n项和为
前n项和为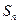 ,满足
,满足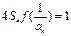 ,
,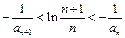 ;
;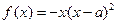 (
(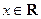 ),其中
),其中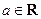 .
.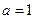 时,求曲线
时,求曲线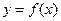 在点
在点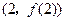 处的切线方程;
处的切线方程;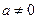 时,求函数
时,求函数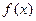 的极大值和极小值;
的极大值和极小值;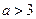 ,
, 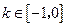 时,若不等式
时,若不等式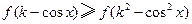 对任意的
对任意的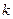 的值。
的值。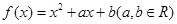 ,若函数在点
,若函数在点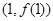 处的切线为
处的切线为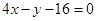 ,数列
,数列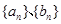 定义:
定义: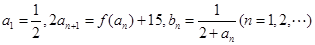 。
。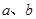 的值;
的值;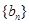 的前
的前 项的和与积分别记为
项的和与积分别记为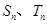 。证明:对任意正整数
。证明:对任意正整数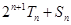 为定值;证明:对任意正整数
为定值;证明:对任意正整数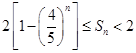 。
。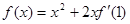 , 则
, 则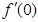 = ( )
= ( )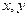 满足
满足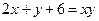 ,则
,则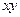 的最小值是________.
的最小值是________.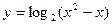 的递增区间是:________________
的递增区间是:________________