题目内容
19.过点P(2,1)作直线l分别交x,y轴于A,B两点,求:(1)|PA|•|PB|取得最小值时l的方程
(2)|OA|•|OB|取得最小值时l的方程.
分析 (1)画出图形,结合图形,设出∠BAO=θ,0°<θ<90°,利用三角函数求出PA、PB的最小值对应的直线l的方程即可;
(2)由题意设直线的截距式方程,利用基本不等式求出|OA|•|OB|取最小值时的直线l的方程即可.
解答 解:(1)如图所示: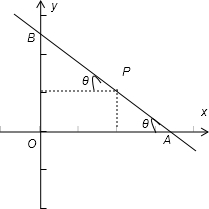
设∠BAO=θ,0°<θ<90°,
则PA=$\frac{1}{sinθ}$,PB=$\frac{2}{cosθ}$,
∴|PA|•|PB|=$\frac{2}{sinθ•cosθ}$=$\frac{4}{sin2θ}$,
∴2θ=90°,即θ=45°时,
|PA|•|PB|取最小值时,直线l的倾斜角为135°,斜率为-1,
直线l的方程为y-1=-1(x-2),
化简得x+y-3=0;
(2)由题意设直线的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a,b>0),
∵直线过P(2,1),∴$\frac{2}{a}$+$\frac{1}{b}$=1,
∴1=$\frac{2}{a}$+$\frac{1}{b}$≥2$\sqrt{\frac{2}{a}•\frac{1}{b}}$=2$\sqrt{\frac{2}{ab}}$,∴ab≥8,
当且仅当$\frac{2}{a}$=$\frac{1}{b}$=$\frac{1}{2}$即a=4且b=2时取等号,
∴|OA|•|OB|的最小值为8,此时直线l的方程为$\frac{x}{4}$+$\frac{y}{2}$=1,
化为一般式方程可得x+2y-4=0.
点评 本题考查直角三角形中的边角关系,三角函数的最值问题,用点斜式求直线的方程,也考查了直线的截距式方程以及基本不等式的应用问题,是中档题目.

练习册系列答案
相关题目
10.已知方程kx+3=log2x的根x0满足x0∈(1,2),则( )
| A. | k<-3 | B. | k>-1 | C. | -3<k<-1 | D. | k<-3或k>-1 |
14.将函数f(x)=cos2x-sin2x的图象向左平移$\frac{π}{8}$个单位后得到函数F(x)的图象,则下列说法正确的是( )
| A. | 函数F(x)是奇函数,最小值是$-\sqrt{2}$ | B. | 函数F(x)是偶函数,最小值是$-\sqrt{2}$ | ||
| C. | 函数F(x)是奇函数,最小值是-2 | D. | 函数F(x)是偶函数,最小值是-2 |
4.函数y=log0.3(x2-2x)的单调递减区间是( )
| A. | (-∞,1) | B. | (-∞,0) | C. | (1,+∞) | D. | (2,+∞) |
8.函数f(x)=$\sqrt{1-{x}^{2}}$的定义域为( )
| A. | [0,1] | B. | (-1,1) | C. | [-1,1] | D. | (-∞,-1]∪[1,+∞) |