题目内容
4.在四面体ABCD中,AB,BC,CD两两垂直,且BC=CD=1,过点B作BH⊥AC,垂足为H,若BH=$\frac{\sqrt{2}}{2}$,求三棱维A-BCD的体积.分析 证明平面ACD内的直线CD,垂直平面ABC内的两条相交直线AB,BC,即可证明CD⊥平面ABC,从而证明平面ACD⊥平面ABC,可得BH⊥平面ACD,求出S△ACD=$\frac{1}{2}×1×\sqrt{2}$=$\frac{\sqrt{2}}{2}$,即可得出结论.
解答 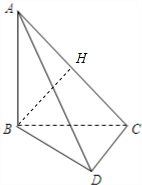 证明:∵CD⊥AB,CD⊥BC,AB∩BC=B,∴CD⊥平面ABC
证明:∵CD⊥AB,CD⊥BC,AB∩BC=B,∴CD⊥平面ABC
又∵CD?平面ACD,∴平面ACD⊥平面ABC,
∴BH⊥平面ACD,
设AB=a,在Rt△BCD中,BD=$\sqrt{2}$,
∴BH=$\frac{AB•BC}{AC}$=$\frac{a}{\sqrt{1+{a}^{2}}}$=$\frac{\sqrt{2}}{2}$,
∴a=1
△ACD中,AC=$\sqrt{2}$,CD=1,AD=$\sqrt{3}$,
∴AC⊥CD,
∴S△ACD=$\frac{1}{2}×1×\sqrt{2}$=$\frac{\sqrt{2}}{2}$,
∴V=$\frac{1}{3}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{6}$
点评 本题考查平面与平面垂直的判定,考查锥体体积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 如图,ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF.
如图,ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF. 已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60°
已知四棱锥P-ABCD中,底面ABCD是菱形,M是PC的中点,∠PDC=90°,∠PDA=90°,∠DAB=60° 如图,已知直三棱柱ABC-A1B1C1中,AB=BC,E为AC中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=BC,E为AC中点.