题目内容
((本小题满分14分)
已知函数 满足
满足 当
当 ,当
,当 的最大值为
的最大值为 。
。
(1)求 时函数
时函数 的解析式;
的解析式;
(2)是否存在实数 使得不等式
使得不等式 对于
对于 若存在,求出实数
若存在,求出实数  的取值集合,若不存在,说明理由.
的取值集合,若不存在,说明理由.
已知函数
 满足
满足 当
当 ,当
,当 的最大值为
的最大值为 。
。(1)求
 时函数
时函数 的解析式;
的解析式;(2)是否存在实数
 使得不等式
使得不等式 对于
对于 若存在,求出实数
若存在,求出实数  的取值集合,若不存在,说明理由.
的取值集合,若不存在,说明理由.解析:(1)由已知得:
 ………………2分
………………2分
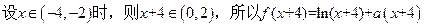
∴
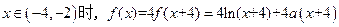 ………………4分
………………4分∴
 ,
, ,∴
,∴ ,
,∴当
 ,
,当
 ,
,∴
 ,∴
,∴
∴当
 时,
时, ………………6分
………………6分(2)由(1)可得:
 时,不等式
时,不等式 恒成立,
恒成立,即为
 恒成立, ………………7分
恒成立, ………………7分①当
 时,
时, ,令
,令
则

令
 ,则当
,则当 时,
时,
∴
 ,∴
,∴ ,
,∴
 ,故此时只需
,故此时只需 即可; ………………10分
即可; ………………10分②当
 时,
时, ,
,令

则

令
 ,则当
,则当 时,
时,
∴
 ,∴
,∴ ,
,∴
 ,故此时只需
,故此时只需 即可, ………………13分
即可, ………………13分 综上所述:
 ,因此满足题中
,因此满足题中 的取值集合为:
的取值集合为: …………14分
…………14分略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 满足
满足 ,且
,且 。
。 上,
上,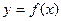 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的范围。
的范围。 满足条件:①
满足条件:① ;②函数
;②函数 的图象与直线
的图象与直线 相切。
相切。 在
在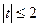 时恒成立,求实数
时恒成立,求实数 的
的 取值范围。
取值范围。 则
则 =" " ;
=" " ; 的定义域为(0,1),求函数
的定义域为(0,1),求函数 的定义域( )
的定义域( )
 ,则
,则 =" "
=" " 
 的零点一定位于如下哪个区间上.( )
的零点一定位于如下哪个区间上.( ) ,则不等式
,则不等式 的解集是:
的解集是:
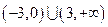



 ( )
( )