题目内容
当0<x≤ 时,4x<logax,则a的取值范围是( )
时,4x<logax,则a的取值范围是( )A.(0,
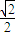 )
)B.(
 ,1)
,1)C.(1,
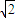 )
)D.(
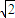 ,2)
,2)
【答案】分析:由指数函数和对数函数的图象和性质,将已知不等式转化为不等式恒成立问题加以解决即可
解答:解:∵0<x≤ 时,1<4x≤2
时,1<4x≤2
要使4x<logax,数形结合可知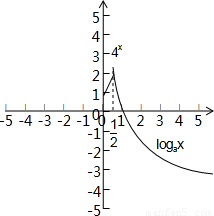
只需2<logax,
∴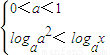
即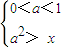 对0<x≤
对0<x≤ 时恒成立
时恒成立
∴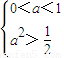
解得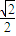 <a<1
<a<1
故选 B
点评:本题主要考查了指数函数和对数函数的图象和性质,不等式恒成立问题的一般解法,属基础题
解答:解:∵0<x≤
 时,1<4x≤2
时,1<4x≤2要使4x<logax,数形结合可知
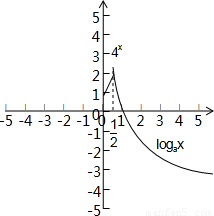
只需2<logax,
∴
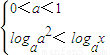
即
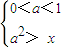 对0<x≤
对0<x≤ 时恒成立
时恒成立∴
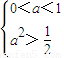
解得
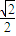 <a<1
<a<1故选 B
点评:本题主要考查了指数函数和对数函数的图象和性质,不等式恒成立问题的一般解法,属基础题

练习册系列答案
相关题目
 时,4x<logax,则a的取值范围是( )
时,4x<logax,则a的取值范围是( )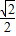 )
)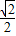 ,1)
,1)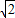 )
)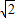 ,2)
,2) 时,4x<logax,则a的取值范围是( )
时,4x<logax,则a的取值范围是( )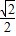 )
)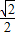 ,1)
,1)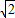 )
)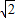 ,2)
,2) 时,4x<logax,则a的取值范围是( )
时,4x<logax,则a的取值范围是( )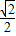 )
)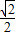 ,1)
,1)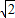 )
)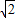 ,2)
,2) 时,4x<logax,则a的取值范围是( )
时,4x<logax,则a的取值范围是( )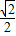 )
)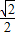 ,1)
,1)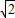 )
) ,2)
,2) 时,4x<logax,则a的取值范围是( )
时,4x<logax,则a的取值范围是( ) )
) ,1)
,1) )
) ,2)
,2)