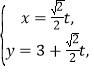题目内容
【题目】动圆
与
相外切，与
相内切．
（1）求动圆圆心的轨迹
的方程；
（2）
是动圆的半径最小时的圆，倾斜角为
且过点
的直线l与相切，与轨迹交于
，
两点，求
的值．
【答案】（1）
（2）
【解析】
（1）根据动圆
与
外切，与
内切，由椭圆定义可知，点的轨迹是以
、
为焦点的椭圆；
（2）由（1）知：
要使半径
最小，则
最小，易知
，
则可设直线方程为
，根据直线与圆
相切求出参数
的值，即可得到直线方程，最后联立直线与椭圆方程，利用弦长公式计算可得.
解：（1）设动圆的半径为，则由题可知：
，
∴
，
由椭圆定义可知点的轨迹是以
，
为焦点，
长轴为6的椭圆，
，
，
，
的轨迹方程为：
（2）由（1）知：要使半径最小，
则最小，易知
由于
，
，圆的方程为：
又由题可得直线
的方程为：，即
到直线的距离为：
，
或
（舍去）
∴直线的方程为：
，联立椭圆方程：消去
整理得：
，设
，
则
，
，
∴
．
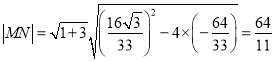练习册系列答案
相关题目
