题目内容
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(2)求线性回归方程,并在散点图中加上回归直线;
(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.
(1)数据对应的散点图如图所示.

(2)所求回归直线方程为 =0.1962x+1.8166.
=0.1962x+1.8166.
(3)销售价格的估计值为 =0.1962×150+1.8166=31.2466(万元).
=0.1962×150+1.8166=31.2466(万元).

(2)所求回归直线方程为
 =0.1962x+1.8166.
=0.1962x+1.8166.(3)销售价格的估计值为
 =0.1962×150+1.8166=31.2466(万元).
=0.1962×150+1.8166=31.2466(万元).试题分析:(1)数据对应的散点图如图所示.

(2)
 =109,
=109, =23.2,
=23.2, (xi-
(xi- )2=1570,
)2=1570, (xi-
(xi- )(yi-
)(yi- )=308,
)=308,设所求的回归直线方程为
 =bx+a,
=bx+a,则b=
 ≈0.1962,
≈0.1962,a=
 -b
-b =23.2-109×
=23.2-109× ≈1.8166,
≈1.8166,故所求回归直线方程为
 =0.1962x+1.8166.
=0.1962x+1.8166.(3)据(2),当x=150 m2时,销售价格的估计值为
 =0.1962×150+1.8166=31.2466(万元).
=0.1962×150+1.8166=31.2466(万元).点评:中档题,确定回归直线方程,关键是准确计算
 等相关元素,对计算能力要求较高。高考题中,常常以填空题形式出现。
等相关元素,对计算能力要求较高。高考题中,常常以填空题形式出现。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 求:
求: (千瓦时)与气温
(千瓦时)与气温 (
( )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
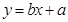 中
中 ,预测当气温为
,预测当气温为 时,用电量约为( )
时,用电量约为( ) =
= x+
x+ ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ). (件)与销售价格
(件)与销售价格 (元/件)存在线性相关关系,根据一组样本数据
(元/件)存在线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为 则下列结论正确的是( )
则下列结论正确的是( )  表示变量
表示变量
 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据,根据表中提供的数据,可求出
(吨标准煤)的几组对应数据,根据表中提供的数据,可求出
 ,则表中
,则表中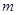 的值为
的值为





 C.
C. ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
 和房屋的面积
和房屋的面积 的数据:
的数据: 
 时的销售价格.
时的销售价格. ,
,  ,
, ,
, )
)