题目内容
过抛物线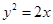 的焦点
的焦点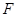 作直线
作直线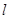 交抛物线于
交抛物线于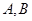 两点,若
两点,若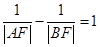 ,则直线
,则直线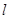 的倾斜角
的倾斜角 。
。
【答案】
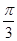 或
或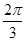
【解析】
试题分析:由题意可得:F(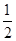 ,0)设A(x1,y1),B(x2,y2).因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,所以|AF|=
,0)设A(x1,y1),B(x2,y2).因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,所以|AF|=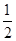 +x1,|BF|=
+x1,|BF|=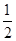 +x2.又因为
+x2.又因为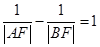 ,所以|AF|<|BF|,即x1<x2,并且直线l的斜率存在.设直线l的方程为y=k(x-
,所以|AF|<|BF|,即x1<x2,并且直线l的斜率存在.设直线l的方程为y=k(x-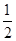 ),联立直线与抛物线的方程可得:k2x2-(k2+2)x+
),联立直线与抛物线的方程可得:k2x2-(k2+2)x+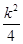 =0,所以x1+x2=
=0,所以x1+x2=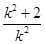 ,x1x2=
,x1x2=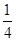 .因为
.因为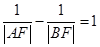 ,所以整理可得
,所以整理可得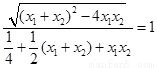 ,即整理可得k4-2k2-3=0,所以解得k2=3.因为0<θ≤
,即整理可得k4-2k2-3=0,所以解得k2=3.因为0<θ≤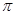 ,所以k=
,所以k=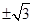 ,即θ=
,即θ=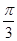 或
或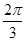
考点:本题考查了直线的倾斜角;抛物线的简单性质.
点评:解决此类问题的关键是熟练掌握抛物线的定义,以及掌握直线与抛物线位置关系,并且结合准确的运算也是解决此类问题的一个重要方面

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
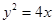 的焦点作直线
的焦点作直线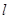 交抛物线于A、B两点,若线段AB中点的横坐标为3,则
交抛物线于A、B两点,若线段AB中点的横坐标为3,则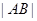 等于
等于 的焦点作直线l交抛物线于A、B两点,若线段
的焦点作直线l交抛物线于A、B两点,若线段 等于( )
等于( )