题目内容
已知等比数列{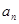 }的前n项和
}的前n项和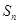 =
=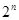 +m(m∈R).
+m(m∈R).
(Ⅰ)求m的值及{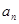 }的通项公式;
}的通项公式;
(Ⅱ)设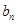 =2
=2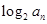 -13,数列{
-13,数列{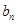 }的前n项和为
}的前n项和为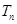 ,求使
,求使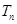 最小时n的值.
最小时n的值.
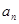 }的前n项和
}的前n项和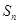 =
=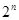 +m(m∈R).
+m(m∈R).(Ⅰ)求m的值及{
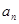 }的通项公式;
}的通项公式;(Ⅱ)设
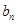 =2
=2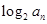 -13,数列{
-13,数列{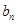 }的前n项和为
}的前n项和为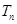 ,求使
,求使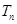 最小时n的值.
最小时n的值.(Ⅰ)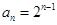 (Ⅱ)
(Ⅱ)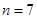 时,
时,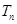 最小.
最小.
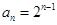 (Ⅱ)
(Ⅱ)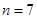 时,
时,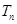 最小.
最小.(I)先利用a1=S1,a2=S2-S1,a3=S3-S2,再利用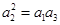 建立关于m的方程求出m的值。
建立关于m的方程求出m的值。
进而求出公比q,求出an.
(2)在(1)的基础上,可求出bn,由于数列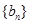 是等差数列,首项为负,公差为正,所以由
是等差数列,首项为负,公差为正,所以由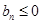 ,可求出Tn最小时n的值
,可求出Tn最小时n的值
(Ⅰ)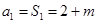 ,
,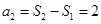 ,
, 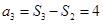 .………………2分
.………………2分
∵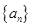 是等比数列, ∴
是等比数列, ∴ 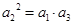 , ∴
, ∴ 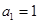 ,
,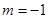 .……4分
.……4分
∵公比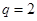 , ∴
, ∴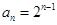 .………6分
.………6分
(Ⅱ)∵ .……………………………………8分
.……………………………………8分
∴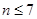 时,
时,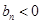 ;
;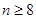 时,
时,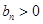 . ∴
. ∴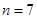 时,
时,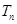 最小
最小
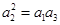 建立关于m的方程求出m的值。
建立关于m的方程求出m的值。进而求出公比q,求出an.
(2)在(1)的基础上,可求出bn,由于数列
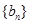 是等差数列,首项为负,公差为正,所以由
是等差数列,首项为负,公差为正,所以由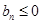 ,可求出Tn最小时n的值
,可求出Tn最小时n的值(Ⅰ)
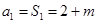 ,
,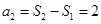 ,
, 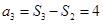 .………………2分
.………………2分∵
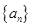 是等比数列, ∴
是等比数列, ∴ 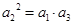 , ∴
, ∴ 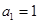 ,
,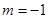 .……4分
.……4分∵公比
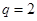 , ∴
, ∴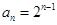 .………6分
.………6分(Ⅱ)∵
 .……………………………………8分
.……………………………………8分∴
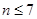 时,
时,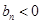 ;
;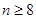 时,
时,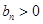 . ∴
. ∴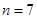 时,
时,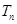 最小
最小
练习册系列答案
相关题目
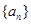 的连续三项,也分别是一个等差数列
的连续三项,也分别是一个等差数列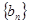 的第一项、第四项、第二十五项.
的第一项、第四项、第二十五项.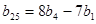 ;(2)求这三个数.
;(2)求这三个数.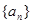 的前
的前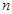 项和
项和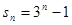 ,则
,则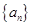 中,
中,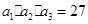 ,
,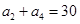 ,
,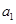 和公比
和公比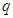 ;(2)前6项的和
;(2)前6项的和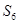 .
. 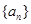 为等比数列,下面结论中正确的是( )
为等比数列,下面结论中正确的是( )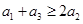
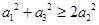
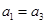 ,则
,则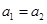
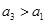 ,则
,则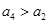
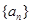 的前
的前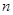 项和为
项和为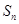 ,若
,若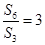 ,则
,则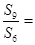 ( )
( )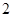
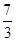
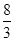
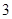
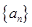 中,已知
中,已知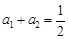 ,
,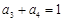 ,则
,则 = .
= .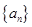 满足:
满足: 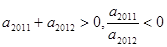 ,则使前
,则使前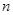 项和
项和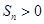 成立的最大自然数
成立的最大自然数 的前
的前 项之和为
项之和为 ,已知
,已知 ,且
,且 ,则
,则 .
.