题目内容
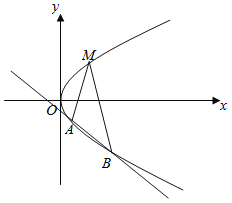
【题目】如图所示,已知点![]() 是抛物线
是抛物线![]() 上一定点,直线
上一定点,直线![]() 的倾斜角互补,且与抛物线另交于
的倾斜角互补,且与抛物线另交于![]() ,
,![]() 两个不同的点.
两个不同的点.
(1)求点![]() 到其准线的距离;
到其准线的距离;
(2)求证:直线![]() 的斜率为定值.
的斜率为定值.
【答案】(1)5;(2)![]()
【解析】
(1)把点M的坐标代入抛物线的方程,求出点M的坐标,然后根据抛物线的定义求出点![]() 到其准线的距离;
到其准线的距离;
(2)设出直线MA的方程,与抛物线方程联立,得出A 的纵坐标,同理得出B的纵坐标,由已知条件结合点差法推导出AB的斜率表达式,把A,B的坐标代入,由此能证明直线AB的斜率为定值.
(1)∵M(a,4)是抛物线y2=4x上一定点,∴42=4a,a=4,
∵抛物线y2=4x的准线方程为x=﹣1,故点M到其准线的距离为5;
(2)由题知直线MA、MB的斜率存在且不为0,设直线MA的方程为:y﹣4=k(x﹣4);
联立![]() ,设
,设![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∵直线![]() 的斜率互为相反数,∴直线MB的方程为:
的斜率互为相反数,∴直线MB的方程为:![]() ,
,
同理可得:![]() ,由A,B两点都在抛物线y2=4x上,∴
,由A,B两点都在抛物线y2=4x上,∴ ![]() ,
,![]() ,
,
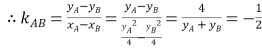 ,
,
∴直线AB的斜率为定值![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目