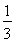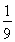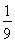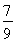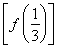题目内容
已知函数f(x)=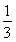 x3+ax2+bx(a,b∈R).
x3+ax2+bx(a,b∈R).
(1)当a=1时,求函数f(x)的单调区间;
(2)若f(1)=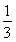 ,且函数f(x)在
,且函数f(x)在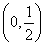 上不存在极值点,求a的取值范围.
上不存在极值点,求a的取值范围.
(1)当b≥1时,f(x)的增区间为(-∞,+∞);当b<1时,f(x)的增区间为(-∞,-1- ),(-1+
),(-1+ ,+∞);减区间为(-1-
,+∞);减区间为(-1- ,-1+
,-1+ ).(2)(-∞,0]
).(2)(-∞,0]
【解析】(1)当a=1时,f′(x)=x2+2x+b.
①若Δ=4-4b≤0,即b≥1时,f′(x)≥0,
所以f(x)为(-∞,+∞)上为增函数,所以f(x)的增区间为(-∞,+∞);
②若Δ=4-4b>0,即b<1时,f′(x)=(x+1+ )(x+1-
)(x+1-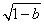 ),
),
所以f(x)在(-∞,-1- ),(-1+
),(-1+ ,+∞)上为增函数,f(x)在(-1-
,+∞)上为增函数,f(x)在(-1- ,-1+
,-1+ )上为减函数.
)上为减函数.
所以f(x)的增区间为(-∞,-1- ),(-1+
),(-1+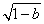 ,+∞),减区间为(-1-
,+∞),减区间为(-1- ,-1+
,-1+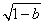 ).
).
综上,当b≥1时,f(x)的增区间为(-∞,+∞);当b<1时,f(x)的增区间为(-∞,-1- ),(-1+
),(-1+ ,+∞);减区间为(-1-
,+∞);减区间为(-1- ,-1+
,-1+ ).
).
(2)由f(1)= ,得b=-a,
,得b=-a,
即f(x)= x3+ax2-ax,f′(x)=x2+2ax-a.
x3+ax2-ax,f′(x)=x2+2ax-a.
令f′(x)=0,即x2+2ax-a=0,变形得(1-2x)a=x2,
因为x∈ ,所以a=
,所以a= .
.
令1-2x=t,则t∈(0,1), =
=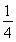
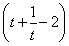 .
.
因为h(t)=t+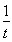 -2在t∈(0,1)上单调递减,故h(t)∈(0,+∞).
-2在t∈(0,1)上单调递减,故h(t)∈(0,+∞).
由y=f(x)在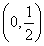 上不存在极值点,得a=
上不存在极值点,得a= 在
在 上无解,所以,a∈(-∞,0].
上无解,所以,a∈(-∞,0].
综上,a的取值范围为(-∞,0]

练习册系列答案
相关题目