题目内容
(本小题满分12分)已知顶点在坐标原点,焦点在 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点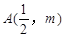 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦 ,
, ,求证:
,求证: 恒过定点
恒过定点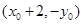 .(3)直线
.(3)直线 与抛物线交于
与抛物线交于 ,
, 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点 ,使得△
,使得△ 为以
为以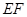 为斜边的直角三角形.
为斜边的直角三角形.
【答案】
(1)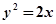 . (2)见解析;(3)
. (2)见解析;(3)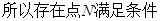
【解析】(1) 设抛物线的方程为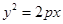 ,则此准线方程为
,则此准线方程为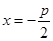 ,根据抛物线的定义可知
,根据抛物线的定义可知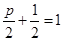 ,从而可知p=1,所以抛物线方程为
,从而可知p=1,所以抛物线方程为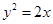 .
.
(2) 由题意知直线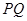 与
与 轴不平行,设
轴不平行,设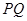 所在直线方程为
所在直线方程为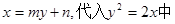 得
得 显然P、Q的纵坐标就是此方程的两个根,然后再由韦达定理可知
显然P、Q的纵坐标就是此方程的两个根,然后再由韦达定理可知 根据
根据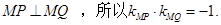 进而得到
进而得到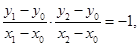 所以
所以 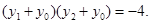 展开整理将韦达定理代入即可得到直线
展开整理将韦达定理代入即可得到直线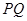 的方程为
的方程为 据此可判定直线PQ一定过定点
据此可判定直线PQ一定过定点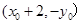 .
.
(3)在(2)的基础上可知若存在N点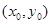 ,则点
,则点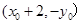 必在直线
必在直线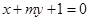 上,所以
上,所以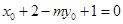 ,因而点N是直线
,因而点N是直线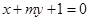 与抛物线
与抛物线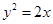 的交点,然后消去y得到关于x的一元二次方程,根据判别式判断此方程组是否有解即可.
的交点,然后消去y得到关于x的一元二次方程,根据判别式判断此方程组是否有解即可.
(1)由题意可设抛物线的方程为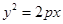 ,则由抛物线的定义可得
,则由抛物线的定义可得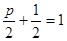 ,即
,即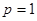 ,所以抛物线的方程为
,所以抛物线的方程为
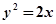 . ……4分
. ……4分
(2)由题意知直线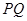 与
与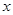 轴不平行,设
轴不平行,设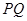 所在直线方程为
所在直线方程为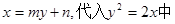 得
得

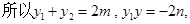 其中
其中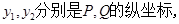
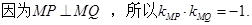
即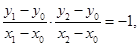 所以
所以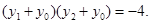

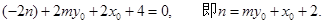
所以直线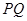 的方程为
的方程为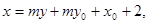
即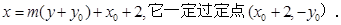
(3)假设
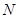 (
(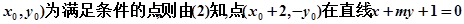 上,
上,
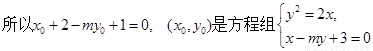 的解,消去
的解,消去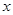 得
得
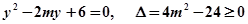

练习册系列答案
相关题目