题目内容
若奇函数f（x）定义域为R，且x≥0时，f（x）=x（x+1），则x∈R时f（x）的解析式为
f（x）=
|
f（x）=
．
|
分析：要求x∈R时f（x）的解析式，只需求出x＜0时f（x）即可．
当x＜0时，-x＞0，由已知表达式可求f（-x），由奇函数性质即可求得（x）．
当x＜0时，-x＞0，由已知表达式可求f（-x），由奇函数性质即可求得（x）．
解答：解：当x＜0时，-x＞0，
则f（-x）=-x（-x+1）=x（x-1），
又f（x）为奇函数，所以f（x）=-f（-x）=-x（x-1）；
综上，f（x）=
．
故答案为：f（x）=
．
则f（-x）=-x（-x+1）=x（x-1），
又f（x）为奇函数，所以f（x）=-f（-x）=-x（x-1）；
综上，f（x）=
|
故答案为：f（x）=
|
点评：本题考查奇函数的性质及函数解析式的求解，属基础题．
练习册系列答案
相关题目
已知奇函数f（x）定义在（﹣1，1）上，且对任意的x1，x2∈（﹣1，1）（x1≠x2），都有
成立，若f（2x﹣1）+f（x﹣1）＞0，则x的取值范围是（ ）
|
| A． | （ | B． | （0，2） | C． | （0，1） | D． | （0， |
，1）
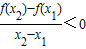成立，若f（2x-1）+f（x-1）＞0，则x的取值范围是（ ）
，1）
）