题目内容
已知点M（-3，0），N（3，0），设P（x，y）是区域C
边界上的点，则下列式子恒成立的是（ ）
|
| A、|PM|+|PN|≥10 |
| B、|PM|-|PN|≥10 |
| C、|PM|+|PN|≤10 |
| D、|PM|+|PN|=10 |
分析：根据题意，分析区域C，计算可得边界线的交点坐标，可将这4个顶点看成椭圆
+
=1的顶点，由椭圆定义知，椭圆上的点到M，N距离之和为10，由图表分析可得|PM|+|PN|应小于10，进而可得答案．
| x2 |
| 25 |
| y2 |
| 16 |
解答：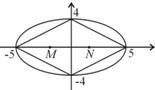
解：C可行域的4个边界交点的坐标为（0，-5），（0，5），（4，0），（-4，0）；
而这四个交点可以看作椭圆
+
=1的四个顶点，
由椭圆定义知，椭圆上的点到M，N距离之和为10，
故|PM|+|PN|≤10，
故选C．
解：C可行域的4个边界交点的坐标为（0，-5），（0，5），（4，0），（-4，0）；而这四个交点可以看作椭圆
| x2 |
| 25 |
| y2 |
| 16 |
由椭圆定义知，椭圆上的点到M，N距离之和为10，
故|PM|+|PN|≤10，
故选C．
点评：本题考查二元一次不等式表示平面区域，注意其中边界的二元一次方程的对应关系，本题中两对关于原点对称，进而发现其交点的对称关系，与椭圆结合，分析可得答案．
练习册系列答案
相关题目
已知点M（-3，0）、N（3，0）、B（1，0），动圆C与直线MN切于点B，过M、N与圆C相切的两直线相交于点P，则P点的轨迹方程为（ ）
A、x2-
| ||
B、x2-
| ||
C、x2+
| ||
D、x2-
|
已知点M（
，0），椭圆
+y2=1与直线y=k（x+
）交于点A、B，则△ABM的周长为（ ）
| 3 |
| x2 |
| 4 |
| 3 |
| A、4 | B、8 | C、12 | D、16 |