题目内容
已知函数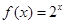 ,
,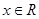 .
.
(Ⅰ)解方程: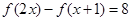 ;
;
(Ⅱ)设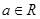 ,求函数
,求函数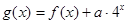 在区间
在区间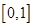 上的最大值
上的最大值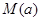 的表达式;
的表达式;
(Ⅲ)若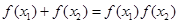 ,
,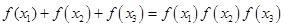 ,求
,求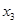 的最大值.
的最大值.
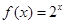 ,
,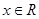 .
.(Ⅰ)解方程:
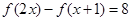 ;
;(Ⅱ)设
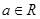 ,求函数
,求函数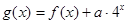 在区间
在区间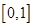 上的最大值
上的最大值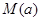 的表达式;
的表达式;(Ⅲ)若
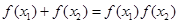 ,
,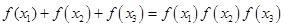 ,求
,求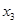 的最大值.
的最大值.(Ⅰ) .(Ⅱ)
.(Ⅱ)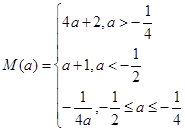 .(Ⅲ)
.(Ⅲ)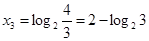 .
.
 .(Ⅱ)
.(Ⅱ)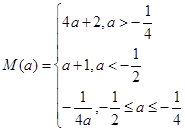 .(Ⅲ)
.(Ⅲ)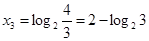 .
.试题分析:(Ⅰ)
 ,
,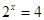 或
或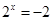 (舍去),
(舍去),所以
 .
.(Ⅱ)
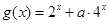 ,
, ,
,令
 ,则
,则 ,
,①当
 时,
时,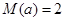 ,
,②当
 时,
时, ,
,若
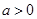 ,则
,则 ,
,若
 ,当
,当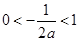 ,即
,即 时,
时, ,
,当
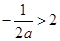 ,即
,即 时,
时, ,
,当
 ,即
,即 时,
时,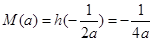 ,
,综上,
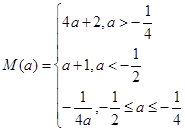 .
.(Ⅲ)由题意知:
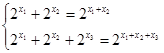
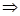
 ,
,所以
 ,
,其中
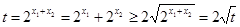 ,所以
,所以 ,
,由
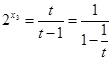 知
知 的最大值是
的最大值是 ,又
,又 单调递增,
单调递增,所以
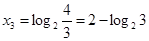 .
.点评:中档题,本题综合考查分段函数的概念,指数函数的性质,二次函数的图象和性质,均值定理的应用。利用换元思想,将问题转化成二次函数问题,通过变换函数表达式,创建应用均值定理的条件,体现应用数学知识的灵活性。

练习册系列答案
相关题目
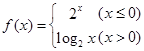 ,则
,则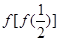 的值等于
的值等于 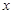 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用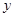 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).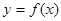 的解析式及其定义域;
的解析式及其定义域; 满足对于
满足对于 时有
时有 恒成立,则称函数
恒成立,则称函数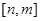 上是“被k限制”,若函数
上是“被k限制”,若函数 在区间
在区间 上是“被2限制”的,则
上是“被2限制”的,则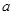 的取值范围为 .
的取值范围为 .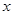 的不等式
的不等式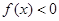 和
和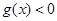 的解集分别为
的解集分别为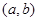 和
和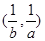 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式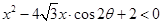 与不等式
与不等式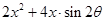
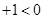 为对偶不等式,且
为对偶不等式,且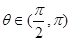 ,那么
,那么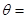 ______.
______. ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数.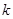 的值,并证明当
的值,并证明当 时,函数
时,函数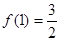 ,函数
,函数 ,
,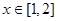 ,求
,求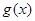 的值域;
的值域; ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得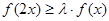 对
对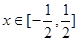 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 有四个不同的零点,则实数
有四个不同的零点,则实数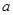 的取值范围是_______________.
的取值范围是_______________.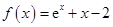 的零点所在的一个区间是( )
的零点所在的一个区间是( )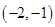
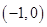
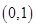
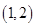
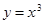 ( )
( ) 上是单调增函数
上是单调增函数