题目内容
有5名同学参加唱歌、跳舞、下棋三项比赛,每项比赛至少有一人参加,每人只能参加一项比赛,若其中某一位同学不能参加跳舞比赛,则参赛方案共有( )A.112种
B.100种
C.92种
D.76种
【答案】分析:分类讨论,跳舞1人,2人,3人,根据分类计数原理得到结果.
解答:解:由题意,若跳舞1人,则有4种方法,再安排其余4人参加唱歌、下棋比赛,有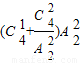 =14,故有56种方法;
=14,故有56种方法;
若跳舞2人,则有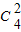 =6种方法,再安排其余3人参加唱歌、下棋比赛,有6种方法,故共有36种方法;
=6种方法,再安排其余3人参加唱歌、下棋比赛,有6种方法,故共有36种方法;
若跳舞3人,则有4种方法,再安排其余2人参加唱歌、下棋比赛,有2种方法,故共有8种方法
故共有100种方法
故选B.
点评:本题考查分类计数问题,解题的关键是正确分类,属于基础题.
解答:解:由题意,若跳舞1人,则有4种方法,再安排其余4人参加唱歌、下棋比赛,有
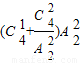 =14,故有56种方法;
=14,故有56种方法;若跳舞2人,则有
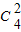 =6种方法,再安排其余3人参加唱歌、下棋比赛,有6种方法,故共有36种方法;
=6种方法,再安排其余3人参加唱歌、下棋比赛,有6种方法,故共有36种方法;若跳舞3人,则有4种方法,再安排其余2人参加唱歌、下棋比赛,有2种方法,故共有8种方法
故共有100种方法
故选B.
点评:本题考查分类计数问题,解题的关键是正确分类,属于基础题.

练习册系列答案
相关题目