题目内容
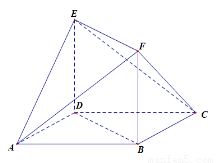
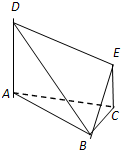
如图所示的多面体中,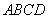 是菱形,
是菱形,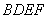 是矩形,
是矩形,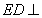 面
面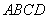 ,
,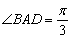 .
.
(1)求证:平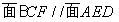 ;
;
(2)若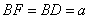 ,求四棱锥
,求四棱锥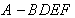 的体积.
的体积.
【答案】
(1)证明过程详见解析;(2) .
.
【解析】
试题分析:
(1)根据面面平行的判断,要证明平面 平面AED,只需要证明面FCB内两条相交的直线FB,BC与面AED平行,而BF与ED平行,BC与AD平行,即可得到两相交直线都与面AED平行,进而得到面面平行.
平面AED,只需要证明面FCB内两条相交的直线FB,BC与面AED平行,而BF与ED平行,BC与AD平行,即可得到两相交直线都与面AED平行,进而得到面面平行.
(2)要求的四棱锥 的体积,必须求的底面BDEF的面积与高,根据
的体积,必须求的底面BDEF的面积与高,根据 、BDEF为矩形可以求的底面积,由于面BDEF与面ABCD是垂直的(DE垂直与底面ABCD),所以可以连接AC与BD交于O,得到AO即为四棱锥的高.可以通过底面为有一个角为60度的菱形求的三角形ABD为等边三角形进而得到高AO的长度,再利用四棱锥的体积公式
、BDEF为矩形可以求的底面积,由于面BDEF与面ABCD是垂直的(DE垂直与底面ABCD),所以可以连接AC与BD交于O,得到AO即为四棱锥的高.可以通过底面为有一个角为60度的菱形求的三角形ABD为等边三角形进而得到高AO的长度,再利用四棱锥的体积公式 ,就求的了四棱锥的体积。
,就求的了四棱锥的体积。
试题解析:
(1)由 是菱形
是菱形


 3分
3分
由 是矩形
是矩形



 6分
6分

(2)连接 ,
,
由 是菱形,
是菱形,
由 面
面 ,
,


 , 10分
, 10分
则 为四棱锥
为四棱锥 的高
的高
由 是菱形,
是菱形, ,
,
则 为等边三角形,
为等边三角形,
由 ;则
;则
 ,
, 14分
14分
考点:面面平行的证明 线面平行 二面角 直二面角 坐标法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形.
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形. (2011•盐城二模)在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形.
(2011•盐城二模)在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形. 如图所示的多面体中,EF丄平面AEB,AE丄EB,AD∥EF,BC∥EF,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点
如图所示的多面体中,EF丄平面AEB,AE丄EB,AD∥EF,BC∥EF,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点 如图所示的多面体中,正方形BB1C1C所在平面垂直平面ABC,△ABC是斜边
如图所示的多面体中,正方形BB1C1C所在平面垂直平面ABC,△ABC是斜边