题目内容
若函数y=ax+b-1（a＞0且a≠1 ）的图象经过一、三、四象限，则正确的是（ ）
分析：利用指数函数的图象过一、三、四象限，先确定函数的单调性，以及b的大小．
解答：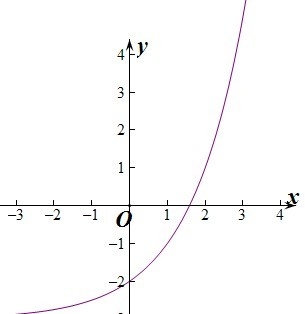
解：因为函数y=ax+b-1（a＞0且a≠1 ）的图象经过一、三、四象限，所以如图：
则由图象可知函数为递增函数，所以a＞1．
当x=0时，y=1+b-1=b＜0．
故选D．
解：因为函数y=ax+b-1（a＞0且a≠1 ）的图象经过一、三、四象限，所以如图：则由图象可知函数为递增函数，所以a＞1．
当x=0时，y=1+b-1=b＜0．
故选D．
点评：本题主要考查指数函数的图象和性质，比较基础．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
若函数y=ax+b的图象如图，则函数y=若函数y=ax+b-1（a＞0且a≠1）的图象不经过第二象限，则有（ ）
| A、a＞1且b＜1 | B、0＜a＜1且b≤1 | C、0＜a＜1且b＞0 | D、a＞1且b≤0 |