题目内容
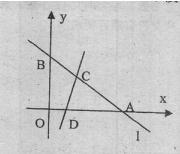 直线l:3x+4y-12=0与x轴和y轴分别交于A,B两点,直线l1和AB,OA分别交于点C,D,且平分△AOB的面积.
直线l:3x+4y-12=0与x轴和y轴分别交于A,B两点,直线l1和AB,OA分别交于点C,D,且平分△AOB的面积.(1)求cos∠BAO的值;
(2)求线段CD长度的最小值.
分析:(1)先根据直线l的方程得到A,B的坐标,进而可得到|0A|、|OB|的长度,进而根据勾股定理求出|AB|的距离,即可得到cos∠BAO的值.
(2)先设|AC|=m,|AD|=n,根据cos∠BAO的值可求其正弦值,再由三角形的面积得到mn的值,再表示出|CD|的表达式结合基本不等式的内容可求得线段CD长度的最小值.
(2)先设|AC|=m,|AD|=n,根据cos∠BAO的值可求其正弦值,再由三角形的面积得到mn的值,再表示出|CD|的表达式结合基本不等式的内容可求得线段CD长度的最小值.
解答: 解:(1)∵l:3x+4y-12=0,令x=0,可得y=3;令y=0,可得x=4;
解:(1)∵l:3x+4y-12=0,令x=0,可得y=3;令y=0,可得x=4;
即|OA|=4,|OB|=3∴AB=
=5,∴cos∠BAO=
=
(2)设|AC|=m,|AD|=n
由cos∠BAO=
,得sin∠BAO=
,
而S△AOB=
×3×4=6
∴S△ACD=
mnsin∠BAO=
mn×
=
S△AOB=
×6=3∴mn=10
又|CD|=
=
=
≥
=
=2(当且仅当m=n时等号成立)
∴线段CD长度的最小值为2
 解:(1)∵l:3x+4y-12=0,令x=0,可得y=3;令y=0,可得x=4;
解:(1)∵l:3x+4y-12=0,令x=0,可得y=3;令y=0,可得x=4;即|OA|=4,|OB|=3∴AB=
| 32+42 |
| AO |
| AB |
| 4 |
| 5 |
(2)设|AC|=m,|AD|=n
由cos∠BAO=
| 4 |
| 5 |
| 3 |
| 5 |
而S△AOB=
| 1 |
| 2 |
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
又|CD|=
| m2+n2-2mncos∠CAD |
m2+n2-2mn×
|
| m2+n2-16 |
≥
| 2mn-16 |
| 2×10-16 |
∴线段CD长度的最小值为2
点评:本题主要考查三角函数中余弦值的求法和余弦定理的应用、基本不等式的应用.考查基础知识的综合应用和灵活应用.三角函数题以基础为主,要强化其基础题得复习.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•江苏二模)选做题
(2012•江苏二模)选做题