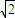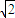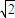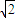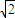题目内容
已知P是直线l:3x-4y+11=0上的动点,PA、PB是圆x2+y2-2x-2y+1=0的两条切线,C是圆心,那么四边形PACB面积的最小值是( )
A、
| ||
B、2
| ||
C、
| ||
D、2
|
分析:把圆的方程化为标准方程为(x-1)2+(y-1)2=1,则可知直线与圆相离.S四边形PACB=S△PAC+S△PBC,当|PC|取最小值时,|PA|=|PB|取最小值,即S△PAC=S△PBC取最小值,由此能够求出四边形PACB面积的最小值.
解答: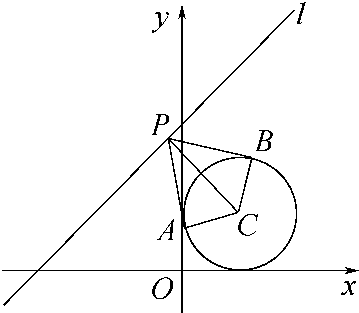 解:把圆的方程化为标准方程为(x-1)2+(y-1)2=1,则可知直线与圆相离.
解:把圆的方程化为标准方程为(x-1)2+(y-1)2=1,则可知直线与圆相离.
如图,S四边形PACB=S△PAC+S△PBC
而S△PAC=
|PA|•|CA|=
|PA|,
S△PBC=
|PB|•|CB|=
|PB|,
又|PA|=
,|PB|=
,
∴当|PC|取最小值时,|PA|=|PB|取最小值,
即S△PAC=S△PBC取最小值,此时,CP⊥l,|CP|=
=2,
则S△PAC=S△PBC=
×
=
,即四边形PACB面积的最小值是
.
故选C.
 解:把圆的方程化为标准方程为(x-1)2+(y-1)2=1,则可知直线与圆相离.
解:把圆的方程化为标准方程为(x-1)2+(y-1)2=1,则可知直线与圆相离.如图,S四边形PACB=S△PAC+S△PBC
而S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
又|PA|=
| |PC|2-1 |
| |PC|2-1 |
∴当|PC|取最小值时,|PA|=|PB|取最小值,
即S△PAC=S△PBC取最小值,此时,CP⊥l,|CP|=
| |3×1-4×1+11| | ||
|
则S△PAC=S△PBC=
| 1 |
| 2 |
| 22-1 |
| ||
| 2 |
| 3 |
故选C.
点评:本题考查直线和圆的位置关系,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,在解答过程中要合理地运用数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目