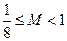题目内容
现有一段长为18m的铁丝,要把它围成一个底面一边长为另一边长2倍的长方体形状的框架,当长方体体积最大时,底面的较短边长是( )
| A.1m | B.1.5m | C.0.75m | D.0.5m |
设该长方体的宽是x米,由题意知,其长是2x米,高是
=
-3x米,(0<x<
)
则该长方体的体积V(x)=x•2x•(
-3x),
由V′(x)=0,得到x=1,
且当0<x<1时,V′(x)>0;
当1<x<
时,V′(x)<0,
即体积函数V(x)在x=1处取得极大值V(1)=3,也是函数V(x)在定义域上的最大值.
所以该长方体体积最大值时,x=1即长方体体积最大时,底面的较短边长是1m.
故选A.
| 18-8x-4x |
| 4 |
| 9 |
| 2 |
| 3 |
| 2 |
则该长方体的体积V(x)=x•2x•(
| 9 |
| 2 |
由V′(x)=0,得到x=1,
且当0<x<1时,V′(x)>0;
当1<x<
| 3 |
| 2 |
即体积函数V(x)在x=1处取得极大值V(1)=3,也是函数V(x)在定义域上的最大值.
所以该长方体体积最大值时,x=1即长方体体积最大时,底面的较短边长是1m.
故选A.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

 ,则
,则 的最小值是( )
的最小值是( )
 ,且
,且 ,若
,若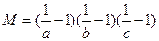 ,则必有( )
,则必有( )