题目内容
对于函数f(x),若存在实数对(a,b),使得等式f(a+x)•f(a-x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.(1)判断函数f(x)=4x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,当x∈[0,2]时,都有1≤g(x)≤3成立,且当x∈[0,1],g(x)=x2+m(1-x)+1(m>0).试求m的取值范围.
【答案】分析:(1)根据给出的新定义,当f(x)=4x时,定义中的等式化为16a=b,显然使该式成立的数对存在,从而说明函数f(x)=4x是“(a,b)型函数”;
(2)由函数g(x)是“(1,4)型函数”,得到g(1+x)g(1-x)=4,变形后得到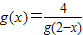 ,若x∈[1,2],则2-x∈[0,1],由函数g(x)在[0,1]上的值域即可得到函数在[1,2]上的值域,而函数g(x)在[0,1]上的解析式已给出,利用分类讨论求出g(x)在[0,1]上的治愈,取并集后结合1≤g(x)≤3求解m的取值范围.
,若x∈[1,2],则2-x∈[0,1],由函数g(x)在[0,1]上的值域即可得到函数在[1,2]上的值域,而函数g(x)在[0,1]上的解析式已给出,利用分类讨论求出g(x)在[0,1]上的治愈,取并集后结合1≤g(x)≤3求解m的取值范围.
解答:解:(1)函数f(x)=4x是“(a,b)型函数”.
因为由f(a+x)•f(a-x)=b,得4a+x•4a-x=16a=b,所以存在这样的实数对,如a=1,b=16.
(2)由题意得,g(1+x)g(1-x)=4,所以当x∈[1,2]时,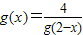 ,其中2-x∈[0,1],
,其中2-x∈[0,1],
而x∈[0,1]时,g(x)=x2+m(1-x)+1=x2-mx+m+1>0,且其对称轴方程为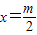 ,
,
①当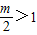 ,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],
,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],
则g(x)在[0,2]上的值域为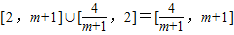 ,
,
由题意得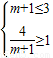 ,此时无解.
,此时无解.
②当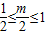 ,即1≤m≤2时,g(x)的值域为
,即1≤m≤2时,g(x)的值域为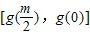 ,即
,即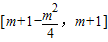 ,
,
所以则g(x)在[0,2]上的值域为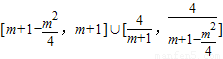 ,
,
则由题意得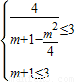 且
且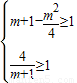 ,解得1≤m≤2.
,解得1≤m≤2.
③当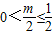 ,即0<m≤1时,g(x)的值域为
,即0<m≤1时,g(x)的值域为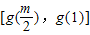 ,即
,即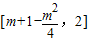 ,
,
则g(x)在[0,2]上的值域为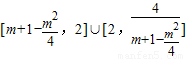 ,
,
=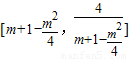 ,
,
则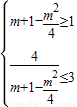 ,解得:
,解得: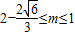 .
.
综上所述,所求m的取值范围是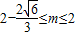 .
.
点评:本题考查了函数的定义域及其求法,考查了函数的值域,考查了分类讨论得数学思想,解答此题的关键是对(2)中函数g(x)的值域的求法,属中档题.
(2)由函数g(x)是“(1,4)型函数”,得到g(1+x)g(1-x)=4,变形后得到
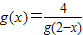 ,若x∈[1,2],则2-x∈[0,1],由函数g(x)在[0,1]上的值域即可得到函数在[1,2]上的值域,而函数g(x)在[0,1]上的解析式已给出,利用分类讨论求出g(x)在[0,1]上的治愈,取并集后结合1≤g(x)≤3求解m的取值范围.
,若x∈[1,2],则2-x∈[0,1],由函数g(x)在[0,1]上的值域即可得到函数在[1,2]上的值域,而函数g(x)在[0,1]上的解析式已给出,利用分类讨论求出g(x)在[0,1]上的治愈,取并集后结合1≤g(x)≤3求解m的取值范围.解答:解:(1)函数f(x)=4x是“(a,b)型函数”.
因为由f(a+x)•f(a-x)=b,得4a+x•4a-x=16a=b,所以存在这样的实数对,如a=1,b=16.
(2)由题意得,g(1+x)g(1-x)=4,所以当x∈[1,2]时,
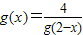 ,其中2-x∈[0,1],
,其中2-x∈[0,1],而x∈[0,1]时,g(x)=x2+m(1-x)+1=x2-mx+m+1>0,且其对称轴方程为
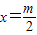 ,
,①当
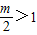 ,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],
,即m>2时,g(x)在[0,1]上的值域为[g(1),g(0)],即[2,m+1],则g(x)在[0,2]上的值域为
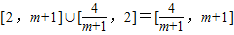 ,
,由题意得
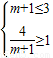 ,此时无解.
,此时无解.②当
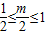 ,即1≤m≤2时,g(x)的值域为
,即1≤m≤2时,g(x)的值域为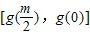 ,即
,即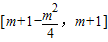 ,
,所以则g(x)在[0,2]上的值域为
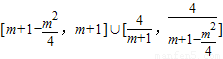 ,
,则由题意得
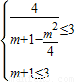 且
且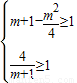 ,解得1≤m≤2.
,解得1≤m≤2.③当
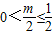 ,即0<m≤1时,g(x)的值域为
,即0<m≤1时,g(x)的值域为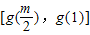 ,即
,即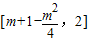 ,
,则g(x)在[0,2]上的值域为
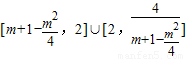 ,
,=
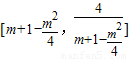 ,
,则
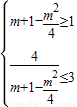 ,解得:
,解得: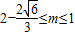 .
.综上所述,所求m的取值范围是
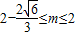 .
.点评:本题考查了函数的定义域及其求法,考查了函数的值域,考查了分类讨论得数学思想,解答此题的关键是对(2)中函数g(x)的值域的求法,属中档题.

练习册系列答案
相关题目