题目内容

给出下列命题：①y=1是幂函数；②函数y=|x+2|-2x在R上有3个零点；③
x-1
(x-2)≥0的解集为[2，+∞）；④当n≤0时，幂函数y=xn的图象与两坐标轴不相交；其中正确的命题是（　　）
分析：根据幂函数的定义对①进行判断；根据函数零点的求法，我们将问题转化为两个基本函数图象交点个数判断后，可以得到②的真假；根据不等式的
x-1
(x-2)≥0的解集对③进行判断；根据幂函数的性质判断出幂函数的指数小于或等于0对④进行判断即可．
解答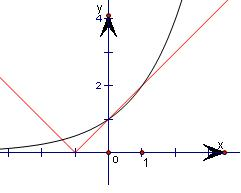：解：：①y=1与幂函数y=x0的定义域不同，故y=1不是幂函数；
②在同一平面坐标系中画出y=2x与函数y=|x+2|的图象，易得两函数的图象共有3个交点，故③函数y=|x+2|-2x在R上有3个零点正确；
③
x-1
(x-2)≥0的解集为[2，+∞）∪{1}，故不正确；
④根据幂函数的性质判断出幂函数的指数小于或等于0时，幂函数y=xn的图象与两坐标轴不相交，正确．
故选C．
点评：本题考查幂函数的性质、函数的零点、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
给出下列命题：①y=lg(sinx+
1+sin2x
)是奇函数；
②若α，β是第一象限角，且α＞β，则cosα＜cosβ；
③函数f（x）=2x-x2在R上有3个零点；
④函数y=sin2x的图象向左平移
π
4
个单位，得到函数y=sin(2x+
π
4
)的图象．
其中正确命题的序号是
 
．（把正确命题的序号都填上）
给出下列命题
①函数y=tan(3x-
π
2
)的周期是
π
3
；
②角α终边上一点P（-3a，4a），且a≠0，那么cosα=-
3
5
；
③函数y=cos(2x-
π
3
)的图象的一个对称中心是(-
π
12
，0)；
④已知f（x）=sin（ωx+2）满足f（x+2）+f（x）=0，则ω=
π
2
．
其中正确的个数有（　　）
给出下列命题：
①y=
x2+3
x2+2
的最小值为2；       
②若a＞b，则
1
a
＜
1
b
成立的充要条件是ab＞0；
③若不等式x2+ax-4＜0对任意x∈（-1，1）恒成立，则实数a的取值范围为（-3，3）．
真命题的序号是
②
②
．
给出下列命题：
①y=tanx在其定义域上是增函数；
②函数y=|sin(2x+
π
3
)|的最小正周期是
π
2
；
③p：
π
4
＜α＜
π
2
；q：f（x）=logtanαx在（0，+∞）内是增函数，则p是q的充分非必要条件；
④函数y=lg(sinx+
sin2x+1
)的奇偶性不能确定．
其中正确命题的序号是（　　）
给出下列命题：
①y=x2是幂函数；
②函数f（x）=2x-x2的零点有2个；
③（x+
1
x
+2）5展开式的项数是6项；
④函数y=sinx（x∈[-π，π]）图象与x轴围成的图形的面积是S=
∫
π
-π
sinxdx；
⑤若ξ～N（1，σ2），且P（0≤ξ≤1）=0.3，则P（ξ≥2）=0.2．
其中真命题的序号是
①⑤
①⑤
（写出所有正确命题的编号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网