Question

椭圆E的中心在原点O，焦点在轴上，其离心率, 过点C（－1,0）的直线与椭圆E相交于A、B两点，且满足点C分向量的比为2.

（1）用直线的斜率k ( k≠0 ) 表示△OAB的面积；（2）当△OAB的面积最大时，求椭圆E的方程。

Answer 1

解：（1）设椭圆E的方程为( a＞b＞0 )，由e =

∴a²=3b²   故椭圆方程x² + 3y² = 3b²

设A(x₁,y₁)、B(x₂,y₂),由于点C（－1，0）分向量的比为2，

① ②

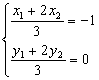∴             即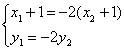

由消去y整理并化简得    (3k²+1)x²+6k²x+3k²－3b²=0

由直线l与椭圆E相交于A（x₁,y₁）, B(x₂,y₂)两点得：

③ ④ ⑤

  

而S_△OAB  ⑤

由①③得:x₂+1=－，代入⑤得：S_△OAB  =

（2）因S_△OAB=,

当且仅当S_△OAB取得最大值

此时 x₁ + x₂ =－1, 又∵  =－1    ∴x₁=1,x₂ =－2

将x₁,x₂及k² = 代入④得3b² = 5 ∴椭圆方程x² + 3y² = 5