题目内容
设全集为实数集合R,集合A={x|1≤x≤4},B={x|m+1≤x≤2m-1}.
(1)当m=3时,求?R(A∪B);
(2)若A∩B=B,求实数m的取值范围.
(1)当m=3时,求?R(A∪B);
(2)若A∩B=B,求实数m的取值范围.
分析:(1)当m=3时,求出集合B,利用集合的基本运算求?R(A∪B);
(2)利用A∩B=B,得到B⊆A,然后根据集合关系确定m的取值范围.
(2)利用A∩B=B,得到B⊆A,然后根据集合关系确定m的取值范围.
解答:解:(1)当m=3时,B={x|4≤x≤5},
∵A={x|1≤x≤4},
∴A∪B={x|1≤x≤4}∪{x|4≤x≤5}={x|1≤x≤5}.
∴?R(A∪B)={x|x<1,或x>5}.
(2)∵A∩B=B,
∴B⊆A.
①当m+1>2m-1,即m<2时,B=∅⊆A,符合题意.
②当m+1≤2m-1,即m≥2时,
若B⊆A,
则
,即
,
∴0≤m≤
.
此时2≤m≤
.
综合可得实数m的取值范围是{m|m≤
}.
∵A={x|1≤x≤4},
∴A∪B={x|1≤x≤4}∪{x|4≤x≤5}={x|1≤x≤5}.
∴?R(A∪B)={x|x<1,或x>5}.
(2)∵A∩B=B,
∴B⊆A.
①当m+1>2m-1,即m<2时,B=∅⊆A,符合题意.
②当m+1≤2m-1,即m≥2时,
若B⊆A,
则
|
|
∴0≤m≤
| 5 |
| 2 |
此时2≤m≤
| 5 |
| 2 |
综合可得实数m的取值范围是{m|m≤
| 5 |
| 2 |
点评:本题主要考查集合的基本运算,以及利用集合关系确定参数问题,将A∩B=B转化为B⊆A是解决本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
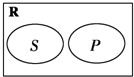 设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},
设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},P={x|5-2a<x<3a},则实数a的取值范围是( )
| A、-5<a<2 | B、1<a<2 | C、1<a≤2 | D、-5≤a≤2 |

 ,则图中阴影部分表示的集合是( )
,则图中阴影部分表示的集合是( )
 B.
B.
 D.
D.
