题目内容
设k<3,k≠0,则二次曲线
-
=1与
+
=1必有( )
| x2 |
| 3-k |
| y2 |
| k |
| x2 |
| 5 |
| y2 |
| 2 |
| A、不同的顶点 |
| B、不同的准线 |
| C、相同的焦点 |
| D、相同的离心率 |
分析:先分类讨论:当0<k<3,和当k<0时,再根据椭圆、双曲线的方程求出焦点坐标,即可得到它们之间的关系,从而得出正确选项.
解答:解:当0<k<3,则0<3-k<3,
∴
-
=1表实轴为x轴的双曲线,a2+b2=3=c2.
∴二曲线有相同焦点;
当k<0时,-k>0,且3-k>-k,
∴
+
=1表焦点在x轴上的椭圆.a2=3-k,b2=-k.
∴a2-b2=3=c2与已知椭圆有相同焦点.
故选C.
∴
| x2 |
| 3-k |
| y2 |
| k |
∴二曲线有相同焦点;
当k<0时,-k>0,且3-k>-k,
∴
| x2 |
| 3-k |
| y2 |
| -k |
∴a2-b2=3=c2与已知椭圆有相同焦点.
故选C.
点评:本题主要考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
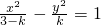 与
与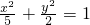 必有
必有 与
与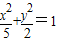 必有( )
必有( )