题目内容
已知(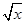
－
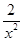)n的展开式中，第五项与第三项的二项式系数之比为14∶3，求展开式中的常数项．
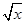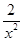－)n的展开式中，第五项与第三项的二项式系数之比为14∶3，求展开式中的常数项．180
依题意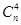
∶
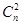＝14∶3，即3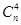＝14，
∴
＝
，
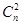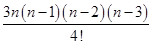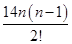∴n＝10.
设第r＋1项为常数项，
又Tr＋1＝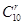
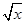()10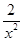－r(－)r
＝(－2)r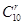
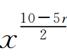
令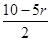
＝0，得r＝2.
∴T3＝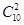
(－2)2＝180，
即常数项为180.
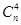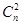∶＝14∶3，即3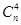＝14，∴
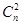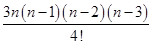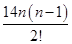＝，∴n＝10.
设第r＋1项为常数项，
又Tr＋1＝
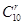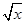()10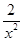－r(－)r＝(－2)r
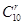
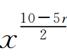
令
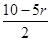＝0，得r＝2.∴T3＝
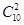(－2)2＝180，即常数项为180.
练习册系列答案
相关题目
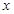，都有
，则
的值是（ ）
n的展开式中第3项的二项式系数是15，则展开式中所有项系数之和为( )
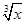＋x2)2n的展开式的二项式系数和比(3x－1)n的展开式的二项式系数和大992，求(2x－
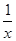)2n的展开式中：
＋
＋…＋
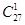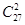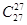除以9的余数为( )
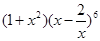展开式中的常数项是 ．
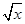)n的展开式中，某一项的系数恰好是它前一项系数的2倍，而且是它后一项系数的
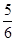，求展开式中二项式系数最大的项．
n(n∈N＋)的展开式中含有常数项的最小的n为( )