题目内容
.本小题满分12分)已知函数
 是R上的奇函数,
是R上的奇函数,
当 时
时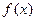 取得极值
取得极值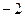 ,
,
(1)求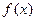 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意 ,不等式
,不等式 恒成立. 、
恒成立. 、
解:∵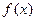 为R上的奇函数,∴
为R上的奇函数,∴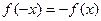 ,
,
即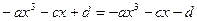 ,∴d=0.∴
,∴d=0.∴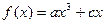 ,
,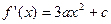 .
.
∵当x=1时,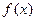 取得极值
取得极值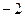 .∴
.∴ ∴
∴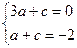 解得:
解得: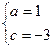 .
.
∴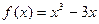 ,
,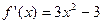 ,
,
令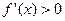 ,则
,则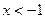 或
或 ,令
,令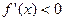 ,则
,则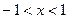 .
.
∴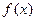 的单调递增区间为
的单调递增区间为 和
和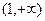 ,单调递减区间为
,单调递减区间为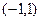 .…………6分
.…………6分
(2)证明:由(1)知,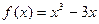 ,(
,(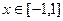 )是减函数,
)是减函数,
且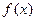 在
在 上的最大值
上的最大值 ,
,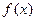 在
在 上的最小值
上的最小值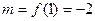 ,
,
∴对任意的 ,恒有
,恒有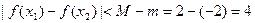 …………12分
…………12分
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目