题目内容
已知
(I)已知数列{an}极限存在且大于零,求
 (将A用a表示);
(将A用a表示);(II)设
 ;
;(III)若
 都成立,求a的取值范围.
都成立,求a的取值范围.
【答案】分析:(I)由

(II) 由此可知
由此可知 .
.
(III) 所以
所以 由此可求出a的取值范围.
由此可求出a的取值范围.
解答:解:(I)由

(II) ∴
∴

(III)
∴
∴

(i)当n=1时结论成立(已验证).
(ii)假设当

故只须证明
 ,
,

∴

即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立.
故
点评:本小题主要考查数列、数列极限的概念和数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力.


(II)
 由此可知
由此可知 .
.(III)
 所以
所以 由此可求出a的取值范围.
由此可求出a的取值范围.解答:解:(I)由


(II)
 ∴
∴

(III)

∴

∴


(i)当n=1时结论成立(已验证).
(ii)假设当


故只须证明

 ,
,
∴


即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立.
故

点评:本小题主要考查数列、数列极限的概念和数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力.

练习册系列答案
相关题目
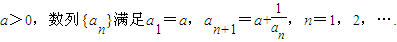
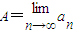 (将A用a表示);
(将A用a表示);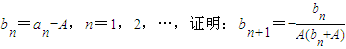 ;
;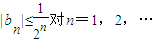 都成立,求a的取值范围.
都成立,求a的取值范围.