题目内容
 已知函数f(x)=x|x-m|(x∈R),且f(1)=0.
已知函数f(x)=x|x-m|(x∈R),且f(1)=0.(1)求m的值,并用分段函数的形式来表示f(x);
(2)在如图给定的直角坐标系内作出函数f(x)的草图(不用列表描点);
(3)由图象指出函数f(x)的单调区间.
分析:(1)根据条件f(1)=0,求m的值即可.
(2)利用函数作出函数图象.
(3)根据函数图象判断函数的单调区间即可.
(2)利用函数作出函数图象.
(3)根据函数图象判断函数的单调区间即可.
解答:解:(1)∵f(1)=0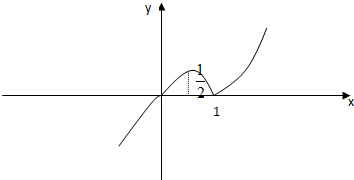 ,
,
∴|m-1|=0,
即m=1;
∴f(x)=x|x-1|=
.
(2)函数图象如图:
(3)函数单调区间:
递增区间:(-∞,
],[1,+∞),
递减区间:[
,1].
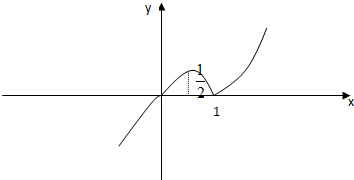 ,
,∴|m-1|=0,
即m=1;
∴f(x)=x|x-1|=
|
(2)函数图象如图:
(3)函数单调区间:
递增区间:(-∞,
| 1 |
| 2 |
递减区间:[
| 1 |
| 2 |
点评:本题主要考查分段函数的应用,考查学生的视图和用图能力,比较基础.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|