题目内容
14.设变量x,y满足约束条件{y≤3x−2x−2y+1≤02x+y≤8,则yx−1的最小值是1.分析 由约束条件作出可行域,利用yx−1的几何意义结合两点连线的斜率得答案.
解答 解:由约束条件件{y≤3x−2x−2y+1≤02x+y≤8作出可行域如图,
联立{x−2y+1=02x+y=8,解得A(3,2),
yx−1的几何意义为可行域内的动点与定点P(1,0)连线的斜率,
则其最小值为kPA=2−03−1=1.
故答案为:1.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
2.已知a=π3,b=3π,c=eπ,则a、b、c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
 和
和 所围成的封闭曲线如图所示,给定点
所围成的封闭曲线如图所示,给定点 ,若在此封闭曲线上恰有三对不同的点,满足每一对点关于点
,若在此封闭曲线上恰有三对不同的点,满足每一对点关于点 对称,则实数
对称,则实数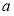 的取值范围是( )
的取值范围是( )
 B.
B. C.
C. D.
D.
 中,
中, ,且数列
,且数列 是等比数列,则
是等比数列,则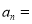 ___________.
___________.