题目内容
(本小题满分12分)已知二次函数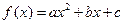 (
(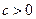 )的导函数的图象如图所示:
)的导函数的图象如图所示:
(Ⅰ)求函数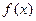 的解析式;
的解析式;
(Ⅱ)令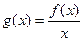 ,求
,求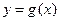 在
在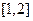 上的最大值.
上的最大值.
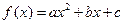 (
(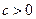 )的导函数的图象如图所示:
)的导函数的图象如图所示:(Ⅰ)求函数
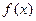 的解析式;
的解析式;(Ⅱ)令
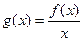 ,求
,求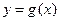 在
在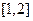 上的最大值.
上的最大值.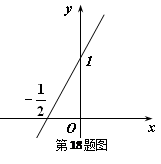
(Ⅰ)函数解析式为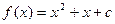 .
.
(Ⅱ)当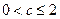 时,
时,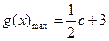 ;当
;当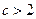 时,
时,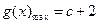 .
.
法二: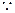 当
当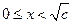 时,
时,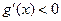 ;当
;当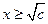 时,
时,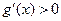 ;
;
∴当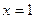 或
或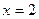 时,
时,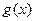 取得最大值,其中
取得最大值,其中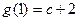 ,
,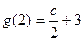 ,
,
当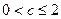 时,
时,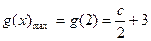 ;当
;当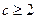 时,
时,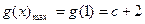 .
.
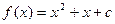 .
.(Ⅱ)当
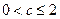 时,
时,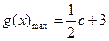 ;当
;当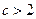 时,
时,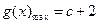 .
. 法二:
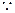 当
当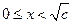 时,
时,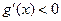 ;当
;当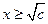 时,
时,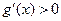 ;
;∴当
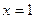 或
或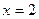 时,
时,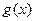 取得最大值,其中
取得最大值,其中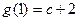 ,
,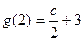 ,
,当
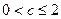 时,
时,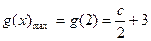 ;当
;当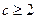 时,
时,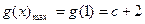 .
. (Ⅰ)因为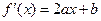 ,由图可知,
,由图可知,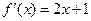 ,
,
∴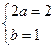 ,得
,得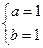 ,故所求函数解析式为
,故所求函数解析式为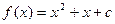 .
.
(Ⅱ)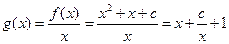 ,
,
则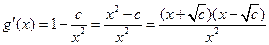 .
.
法一:①若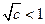 ,即
,即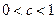 时,
时,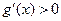 ,
,
∴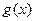 在
在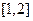 上是增函数,故
上是增函数,故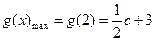 .
.
②若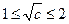 ,即
,即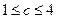 ,当
,当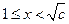 时,
时,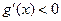 ;当
;当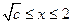 时,
时,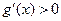 ;
;
∵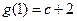 ,
,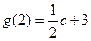 ,
,
∴当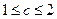 时,
时,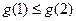 ,
,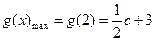 ;
;
当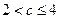 时,
时,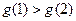 ,
,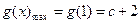 .
.
③若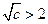 ,即
,即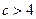 时,
时,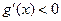 ,
,
∴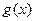 在
在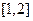 上是减函数,故
上是减函数,故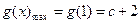 .
.
综上所述,当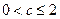 时,
时,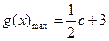 ;当
;当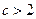 时,
时,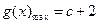 .
.
法二: 当
当 时,
时, ;当
;当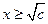 时,
时,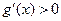 ;
;
∴当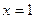 或
或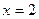 时,
时,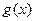 取得最大值,其中
取得最大值,其中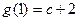 ,
,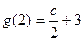 ,
,
当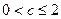 时,
时,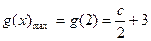 ;当
;当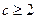 时,
时,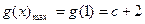 .
.
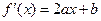 ,由图可知,
,由图可知,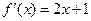 ,
, ∴
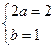 ,得
,得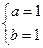 ,故所求函数解析式为
,故所求函数解析式为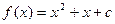 .
.(Ⅱ)
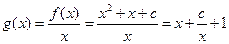 ,
,则
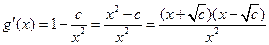 .
.法一:①若
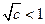 ,即
,即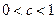 时,
时,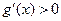 ,
,∴
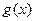 在
在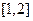 上是增函数,故
上是增函数,故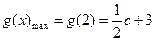 .
. ②若
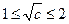 ,即
,即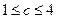 ,当
,当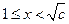 时,
时,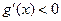 ;当
;当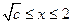 时,
时,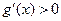 ;
;∵
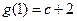 ,
,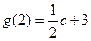 ,
,∴当
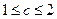 时,
时,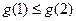 ,
,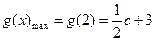 ;
;当
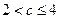 时,
时,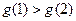 ,
,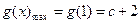 .
. ③若
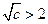 ,即
,即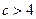 时,
时,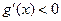 ,
,∴
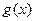 在
在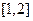 上是减函数,故
上是减函数,故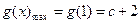 .
. 综上所述,当
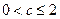 时,
时,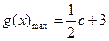 ;当
;当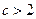 时,
时,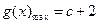 .
. 法二:
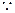 当
当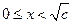 时,
时,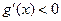 ;当
;当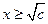 时,
时,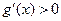 ;
;∴当
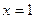 或
或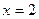 时,
时,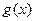 取得最大值,其中
取得最大值,其中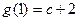 ,
,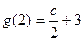 ,
,当
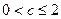 时,
时,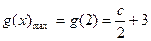 ;当
;当 时,
时, .
. 
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
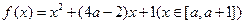 的最小值为
的最小值为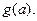 求函数
求函数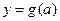 的解析式。
的解析式。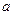 为实数,函数
为实数,函数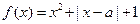 ,
,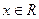 .
. 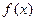 的奇偶性; (2)求
的奇偶性; (2)求 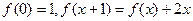
 .
. 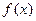 ;
;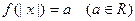 的解的个数.
的解的个数.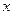 ∈[0,2]时,函数
∈[0,2]时,函数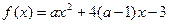 在
在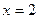 时取得最大值,则a的取值范围是
时取得最大值,则a的取值范围是
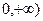


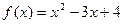 ,其中
,其中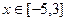 ,则函数
,则函数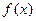 的值域为( )
的值域为( )



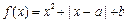 在区间
在区间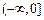 上为减函数,则实数
上为减函数,则实数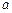 的取值范围是( )
的取值范围是( )



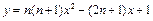 ,当n依次取1,2,3,4,…,n,…时,图象在x轴上截得的线段的长度的总和为
,当n依次取1,2,3,4,…,n,…时,图象在x轴上截得的线段的长度的总和为