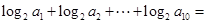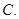题目内容
已知数列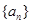 中,
中,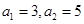 ,其前
,其前 项和
项和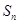 满足:
满足: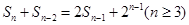 ,令
,令
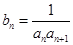 .
.
(1) 求数列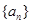 的通项公式;
的通项公式;
(2) 若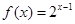 ,求证:
,求证: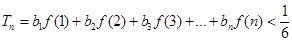 ;
;
(3) 令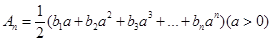 ,问是否存在正实数
,问是否存在正实数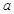 同时满足下列两个条件?
同时满足下列两个条件?
①对任意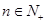 ,都有
,都有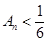 ;
;
②对任意的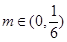 ,均存在
,均存在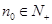 ,使得当
,使得当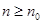 时总有
时总有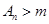 .
.
若存在,求出所有的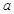 ; 若不存在,请说明理由.
; 若不存在,请说明理由.
 中,
中,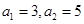 ,其前
,其前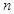 项和
项和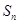 满足:
满足: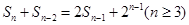 ,令
,令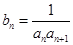 .
.(1) 求数列
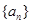 的通项公式;
的通项公式;(2) 若
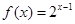 ,求证:
,求证: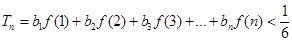 ;
;(3) 令
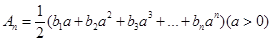 ,问是否存在正实数
,问是否存在正实数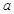 同时满足下列两个条件?
同时满足下列两个条件?①对任意
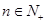 ,都有
,都有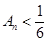 ;
;②对任意的
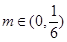 ,均存在
,均存在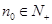 ,使得当
,使得当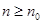 时总有
时总有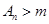 .
.若存在,求出所有的
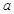 ; 若不存在,请说明理由.
; 若不存在,请说明理由. (1) 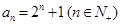 . (2)略 (3)存在正实数
. (2)略 (3)存在正实数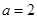 符合题意.
符合题意.
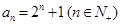 . (2)略 (3)存在正实数
. (2)略 (3)存在正实数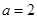 符合题意.
符合题意.本试题主要是考查了数列的求和和数列的通项公式的运用,不等式的证明。
(1)由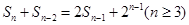 得
得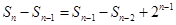
即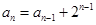 ,移项得
,移项得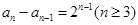 ,
,
∴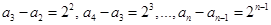 ,这
,这 个等式叠加可得
个等式叠加可得
可得结论,
(2)由(1)知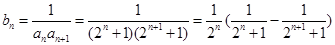 ,
,
又 , ∴
, ∴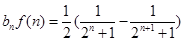 故相加得证。
故相加得证。
(3)当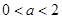 时,
时,
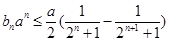 ,
,
∴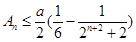 .
.
由2)知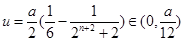 ,即
,即 , 而此时
, 而此时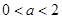 ,可见存在实数a=2满足题意
,可见存在实数a=2满足题意
(1)由
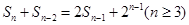 得
得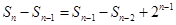
即
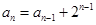 ,移项得
,移项得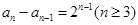 ,
,∴
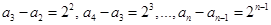 ,这
,这 个等式叠加可得
个等式叠加可得可得结论,
(2)由(1)知
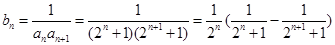 ,
,又
 , ∴
, ∴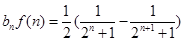 故相加得证。
故相加得证。(3)当
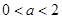 时,
时,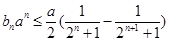 ,
,∴
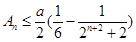 .
.由2)知
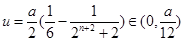 ,即
,即 , 而此时
, 而此时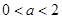 ,可见存在实数a=2满足题意
,可见存在实数a=2满足题意
练习册系列答案
相关题目
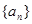 中,
中,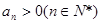 ,公比
,公比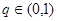 ,且
,且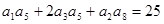 ,
,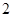 是
是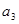 与
与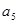 的等比中项。设
的等比中项。设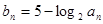 .
.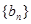 的通项公式;
的通项公式;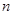 项和为
项和为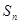 ,
,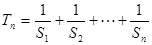 ,求
,求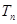 .
. 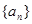 中,a1=3,前三项和为21,则a3 + a4 + a5 等于
中,a1=3,前三项和为21,则a3 + a4 + a5 等于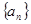 为等比数列,
为等比数列,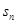 是它的前
是它的前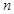 项和,若
项和,若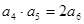 ,
,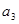 、
、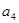 的等比中项为
的等比中项为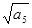 ,则
,则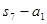 =( )
=( )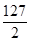
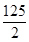
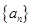 的前
的前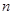 项和为
项和为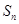 ,若
,若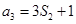 ,
,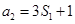 ,则公比
,则公比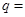
 中
中 >0,且
>0,且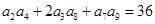 ,则
,则 =
= 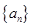 的各项均为正数,且
的各项均为正数,且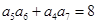 ,则
,则