题目内容
已知函数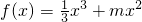 ,其中m为实数.
,其中m为实数.
(1)函数f(x)在x=-1处的切线斜率为 ,求m的值;
,求m的值;
(2)求f(x)的单调区间;
(3)若f(x)在x=-2处取得极值,直线y=a与y=f(x)的图象有三个不同的交点,求a的取值范围.
解:(1)f'(x)=x2+2mx,f'(-1)=1-2m
由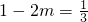 ,解得
,解得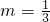 .
.
(2)f'(x)=x2+2mx=x(x+2m)
①当m=0时,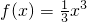 ,在(-∞,+∞)上单调递增;
,在(-∞,+∞)上单调递增;
②当m>0时x变化时,f'(x),f(x)的变化状态如下表:
函数f(x)的单调递增区间是(-∞,-2m)和(0,+∞),单调递减区间是(-2m,0).
当m<0时x变化时,f'(x),f(x)的变化状态如下表:
函数f(x)的单调递增区间是(-∞,0)和(-2m,+∞),单调递减区间是(0,-2m).
综上:当m=0时,f(x)的单调递增区间是(-∞,+∞);
当m>0时,f(x)的单调递增区间是(-∞,-2m)和(0,+∞),单调递减区间是(-2m,0);
当m<0时,f(x)的单调递增区间是(-∞,0)和(-2m,+∞),单调递减区间是(0,-2m).
(3)由题意f'(-2)=0,解得m=1.
所以,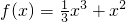
由(2)知f(x)在区间(-∞,-2)上递增,在(-2,0)上递减,(0,+∞)上递增
所以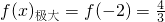 ,f(x)极小=f(0)=0,
,f(x)极小=f(0)=0,
要使直线y=a与y=f(x)的图象有三个不同的交点
只需,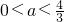 .
.
分析:(1)求出函数的导函数,由已知在x=-1处f(x)的切线斜率为 ,代入可得f'(-1)=
,代入可得f'(-1)= ,进一步得到m的值.
,进一步得到m的值.
(2)利用导数f′(x)=x2+2mx,对参数m要分m=0,m>0,m<0三种情况来讨论,可借助于x,f'(x),f(x)的变化情况表来解得函数的单调区间.
(3)f(x)在x=-2处取得极值,即有f'(-2)=0可得到m的值,代入函数解析式y=f(x)求得极值,由函数的图象与直线有三个不同的交点,寻求函数的极值点,得到极值,通过比较函数的极值于参数a之间的关系即可得到结论.
点评:本题考查函数的导数以及导数的几何意义,利用导数求解函数的单调性和极值问题,考查了二次函数的性质,综合考查了函数与方程的思想,转化与化归的思想,以及分类讨论等数学思想,在求含参数的函数的单调区间时对学生的能力有较高的要求.
由
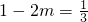 ,解得
,解得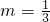 .
.(2)f'(x)=x2+2mx=x(x+2m)
①当m=0时,
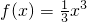 ,在(-∞,+∞)上单调递增;
,在(-∞,+∞)上单调递增;②当m>0时x变化时,f'(x),f(x)的变化状态如下表:
| x | (-∞,-2m) | -2m | (-2m,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
当m<0时x变化时,f'(x),f(x)的变化状态如下表:
| x | (-∞,0) | 0 | (0,-2m) | -2m | (-2m,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
综上:当m=0时,f(x)的单调递增区间是(-∞,+∞);
当m>0时,f(x)的单调递增区间是(-∞,-2m)和(0,+∞),单调递减区间是(-2m,0);
当m<0时,f(x)的单调递增区间是(-∞,0)和(-2m,+∞),单调递减区间是(0,-2m).
(3)由题意f'(-2)=0,解得m=1.
所以,
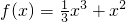
由(2)知f(x)在区间(-∞,-2)上递增,在(-2,0)上递减,(0,+∞)上递增
所以
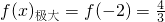 ,f(x)极小=f(0)=0,
,f(x)极小=f(0)=0,要使直线y=a与y=f(x)的图象有三个不同的交点
只需,
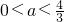 .
.分析:(1)求出函数的导函数,由已知在x=-1处f(x)的切线斜率为
 ,代入可得f'(-1)=
,代入可得f'(-1)= ,进一步得到m的值.
,进一步得到m的值.(2)利用导数f′(x)=x2+2mx,对参数m要分m=0,m>0,m<0三种情况来讨论,可借助于x,f'(x),f(x)的变化情况表来解得函数的单调区间.
(3)f(x)在x=-2处取得极值,即有f'(-2)=0可得到m的值,代入函数解析式y=f(x)求得极值,由函数的图象与直线有三个不同的交点,寻求函数的极值点,得到极值,通过比较函数的极值于参数a之间的关系即可得到结论.
点评:本题考查函数的导数以及导数的几何意义,利用导数求解函数的单调性和极值问题,考查了二次函数的性质,综合考查了函数与方程的思想,转化与化归的思想,以及分类讨论等数学思想,在求含参数的函数的单调区间时对学生的能力有较高的要求.

练习册系列答案
相关题目
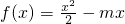 ,其中m为实常数.
,其中m为实常数. 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;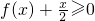 的解集.
的解集.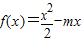 ,其中m为实常数.
,其中m为实常数.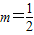 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;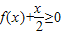 的解集.
的解集.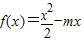 ,其中m为实常数.
,其中m为实常数.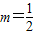 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;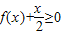 的解集.
的解集.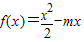 ,其中m为实常数.
,其中m为实常数.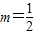 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;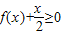 的解集.
的解集.