题目内容
已知函数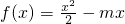 ,其中m为实常数.
,其中m为实常数.
(1)当 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;
(2)当m变化时,讨论关于x的不等式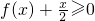 的解集.
的解集.
解(1)当 时,由f(x)<x,
时,由f(x)<x,
得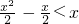 ,
,
即x(x-3)<0.
∴不等式的解集是{x|0<x<3},
(2)由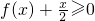 ,
,
得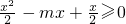 ,
,
即x[x-(2m-1)]≥0.
当2m-1>0,即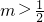 时,不等式的解集为{x|x≤0或x≥2m-1};
时,不等式的解集为{x|x≤0或x≥2m-1};
当2m-1<0,即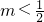 时,不等式的解集为{x|x≥0或x≤2m-1};
时,不等式的解集为{x|x≥0或x≤2m-1};
当2m-1=0,即 时,不等式的解集为R.
时,不等式的解集为R.
分析:(1)将m的值代入函数f(x)中,列出不等式是一个二次不等式,求出相应的二次方程的根,据二次方程根的形式写出其解集.
(2)通过因式分解得到二次不等式相应的两个根0,2m-1,通过讨论m的范围得到两个根的大小,据二次不等式的解集形式写出解集.
点评:求二次不等式的解问题,若含参数一般需要讨论,一般从二次项系数的符号、判别式的符号、两个根的大小三个方面进行讨论,属于难题.
 时,由f(x)<x,
时,由f(x)<x,得
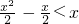 ,
,即x(x-3)<0.
∴不等式的解集是{x|0<x<3},
(2)由
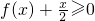 ,
,得
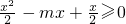 ,
,即x[x-(2m-1)]≥0.
当2m-1>0,即
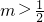 时,不等式的解集为{x|x≤0或x≥2m-1};
时,不等式的解集为{x|x≤0或x≥2m-1}; 当2m-1<0,即
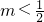 时,不等式的解集为{x|x≥0或x≤2m-1};
时,不等式的解集为{x|x≥0或x≤2m-1}; 当2m-1=0,即
 时,不等式的解集为R.
时,不等式的解集为R.分析:(1)将m的值代入函数f(x)中,列出不等式是一个二次不等式,求出相应的二次方程的根,据二次方程根的形式写出其解集.
(2)通过因式分解得到二次不等式相应的两个根0,2m-1,通过讨论m的范围得到两个根的大小,据二次不等式的解集形式写出解集.
点评:求二次不等式的解问题,若含参数一般需要讨论,一般从二次项系数的符号、判别式的符号、两个根的大小三个方面进行讨论,属于难题.

练习册系列答案
相关题目
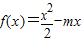 ,其中m为实常数.
,其中m为实常数.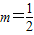 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;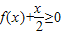 的解集.
的解集.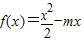 ,其中m为实常数.
,其中m为实常数.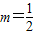 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;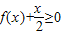 的解集.
的解集.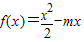 ,其中m为实常数.
,其中m为实常数.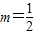 时,求不等式f(x)<x的解集;
时,求不等式f(x)<x的解集;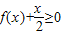 的解集.
的解集.