题目内容
(本题满分12分)已知函数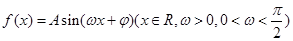 的部分图像如图所示.
的部分图像如图所示.
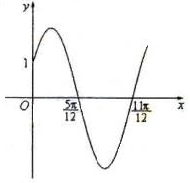
(Ⅰ)求函数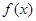 的解析式;
的解析式;
(Ⅱ)求函数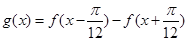 的单调递增区间.
的单调递增区间.
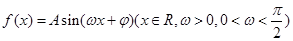 的部分图像如图所示.
的部分图像如图所示.
(Ⅰ)求函数
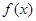 的解析式;
的解析式;(Ⅱ)求函数
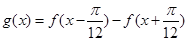 的单调递增区间.
的单调递增区间.(Ⅰ)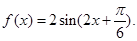 (Ⅱ)单调递增区间是
(Ⅱ)单调递增区间是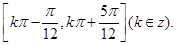
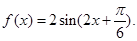 (Ⅱ)单调递增区间是
(Ⅱ)单调递增区间是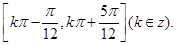
本试题主要是考查了通过图像求解解析式和研究三角函数的图像与性质的综合运用。
(1)由题设图像知,周期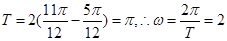 .
.
因为点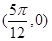 在函数图像上,所以
在函数图像上,所以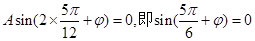 .
.
又 即
即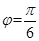 .
.
从而得到解析式
(2)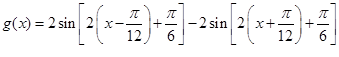 化为单一函数为
化为单一函数为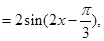 然后利用单调性得到结论。
然后利用单调性得到结论。
(Ⅰ)由题设图像知,周期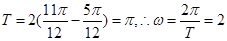 .
.
因为点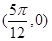 在函数图像上,所以
在函数图像上,所以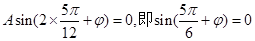 .
.
又 即
即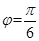 .
.
又点 在函数图像上,所以
在函数图像上,所以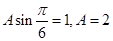 ,故函数f(x)的解析式为
,故函数f(x)的解析式为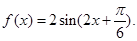
(Ⅱ)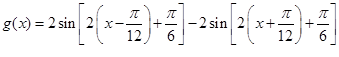
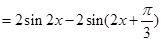
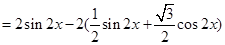
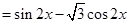
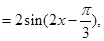
由 得
得
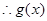 的单调递增区间是
的单调递增区间是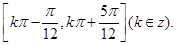
(1)由题设图像知,周期
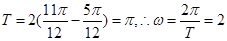 .
.因为点
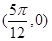 在函数图像上,所以
在函数图像上,所以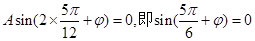 .
.又
 即
即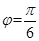 .
.从而得到解析式
(2)
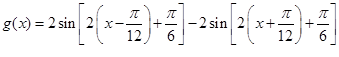 化为单一函数为
化为单一函数为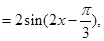 然后利用单调性得到结论。
然后利用单调性得到结论。(Ⅰ)由题设图像知,周期
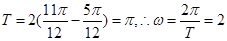 .
.因为点
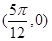 在函数图像上,所以
在函数图像上,所以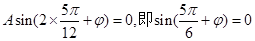 .
.又
 即
即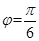 .
.又点
 在函数图像上,所以
在函数图像上,所以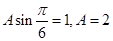 ,故函数f(x)的解析式为
,故函数f(x)的解析式为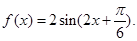
(Ⅱ)
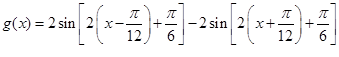
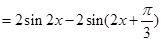
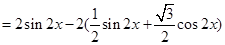
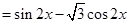
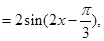
由
 得
得
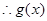 的单调递增区间是
的单调递增区间是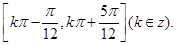

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

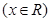 的图象经过点
的图象经过点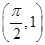 .
.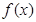 的解析式,并求函数的最小正周期.
的解析式,并求函数的最小正周期. 且
且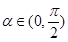 ,求
,求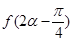 的值。
的值。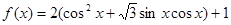 .
.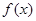 的最小正周期,并求其单调递增区间;
的最小正周期,并求其单调递增区间;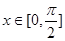 时,求
时,求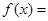
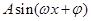 (其中A>0,
(其中A>0,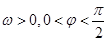 )的图象如图所示.
)的图象如图所示.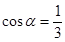 ,求
,求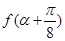 的值.
的值.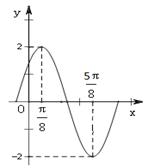
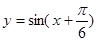 图象上各点的横坐标缩短到原来的
图象上各点的横坐标缩短到原来的 倍
倍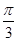 个单位,那么所得图象的一条对称轴方程为
个单位,那么所得图象的一条对称轴方程为 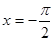
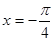
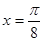

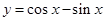 的图象可由函数
的图象可由函数 的图象( )
的图象( ) 平移个长度单位
平移个长度单位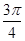 平移个长度单位
平移个长度单位 设函数
设函数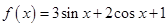 ,若实数
,若实数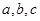 使得
使得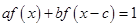 对任意实数
对任意实数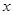 恒成立,则
恒成立,则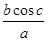 的值等于( )
的值等于( )
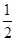


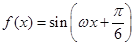 的导函数
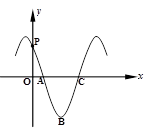
的导函数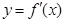 的部分图像如图所示:图象与
的部分图像如图所示:图象与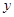 轴交点
轴交点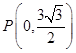 ,与x轴正半轴的两交点为A、C,B为图象的最低点 ,则
,与x轴正半轴的两交点为A、C,B为图象的最低点 ,则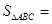 ___ ___ .
___ ___ .
 的图象如图所示,则
的图象如图所示,则 .
.