题目内容
函数 的定义域为D,若对任意的
的定义域为D,若对任意的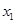 、
、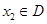 ,当
,当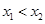 时,都有
时,都有 ,则称函数
,则称函数 在D上为“非减函数”.设函数
在D上为“非减函数”.设函数 在
在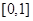 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2)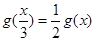 ;(3)
;(3)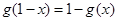 ,则
,则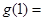 、
、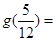 .
.
【答案】
1、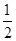
【解析】
试题分析:根据题意,由于函数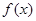 的定义域为D,若对任意的
的定义域为D,若对任意的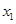 、
、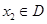 ,当
,当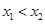 时,都有
时,都有 ,则称函数
,则称函数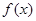 在D上为“非减函数”.设函数
在D上为“非减函数”.设函数 在
在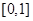 上为“非减函数”,且满足以下三个条件(1)
上为“非减函数”,且满足以下三个条件(1)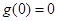 ;(2)
;(2)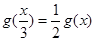 ;(3)
;(3)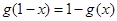 ,那么可知g(1)=1-g(0)=1,
,那么可知g(1)=1-g(0)=1,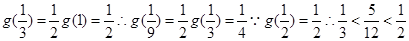 , 因为当
, 因为当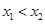 时,都有
时,都有 ,那么说明了函数为常函数,故
,那么说明了函数为常函数,故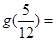
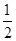 ,故答案为1、
,故答案为1、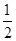
考点:抽象函数及其应用
点评:本题考查的知识点是抽象函数及其应用,其中根据已知中,函数满足的条件,是解答本题的关键

练习册系列答案
相关题目
 的定义域为D,若对于任意
的定义域为D,若对于任意
 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 ;②
;② ;③
;③ .则
.则 等于( )
等于( ) B.
B. C.
C. D.无法确定
D.无法确定 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b] D,使得函数
D,使得函数 ; ②、
; ②、 ;
; ; ④、
; ④、 .
. 的定义域为D,若对任意的
的定义域为D,若对任意的 、
、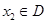 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在
在 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2) ;(3)
;(3) ,则
,则 、
、 .
.