题目内容
函数 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b] D,使得函数
D,使得函数 满足:(1)
满足:(1) 在[a,b]内是单调函数;(2)
在[a,b]内是单调函数;(2) 在[a,b]上的值域为[2a,2b],则称区间[a,b]为y=
在[a,b]上的值域为[2a,2b],则称区间[a,b]为y= 的“美丽区间”.下列函数中存在“美丽区间”的是
. (只需填符合题意的函数序号)
的“美丽区间”.下列函数中存在“美丽区间”的是
. (只需填符合题意的函数序号)
①、 ; ②、
; ②、 ;
;
③、 ; ④、
; ④、 .
.
【答案】
①③④
【解析】
试题分析:函数中存在“美丽区间”的定义可知:① 在[a,b]内是单调增函数;
在[a,b]内是单调增函数;
则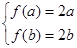 ,解得
,解得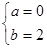 ∴f(x)=x2(x≥0),若存在“美丽区间”[0,2],∴f(x)=x2(x≥0),若存在“美丽区间”[0,2];②f(x)=ex(x∈R),若存在“美丽区间”[a,b],则
∴f(x)=x2(x≥0),若存在“美丽区间”[0,2],∴f(x)=x2(x≥0),若存在“美丽区间”[0,2];②f(x)=ex(x∈R),若存在“美丽区间”[a,b],则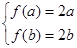 ,所以
,所以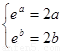 ,构建函数g(x)=ex-2x,∴g′(x)=ex-2,∴函数在(-∞,ln2)上单调减,在(ln2,+∞)上单调增,∴函数在x=ln2处取得极小值,且为最小值.∵g(ln2)=2-2ln2>0,∴g(x)>0恒成立,∴ex-2x=0无解,故函数不存在“美丽区间”;③
,构建函数g(x)=ex-2x,∴g′(x)=ex-2,∴函数在(-∞,ln2)上单调减,在(ln2,+∞)上单调增,∴函数在x=ln2处取得极小值,且为最小值.∵g(ln2)=2-2ln2>0,∴g(x)>0恒成立,∴ex-2x=0无解,故函数不存在“美丽区间”;③ 在
在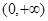 上单调递减,若存在“美丽区间”[a,b],则
上单调递减,若存在“美丽区间”[a,b],则 ,则
,则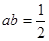 ,故存在;④
,故存在;④ ,
, ,若存在“倍值区间”[a,b]⊆[0,1],则
,若存在“倍值区间”[a,b]⊆[0,1],则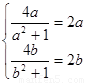 ∴a=0,b=1,若存在“美丽区间”[0,1];故存在“美丽区间”的是①③④.
∴a=0,b=1,若存在“美丽区间”[0,1];故存在“美丽区间”的是①③④.
考点:1.函数的值域 ;2.函数的单调性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域为D,若对于任意
的定义域为D,若对于任意
 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 ;②
;② ;③
;③ .则
.则 等于( )
等于( ) B.
B. C.
C. D.无法确定
D.无法确定 的定义域为D,若对任意的
的定义域为D,若对任意的 、
、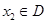 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在
在 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2) ;(3)
;(3) ,则
,则 、
、 .
.