题目内容
已知数列{an}中Sn是它的前n项和,且Sn+1=4an+2(n∈N*),a1=1。
(1)设bn=an+1-2an(n∈N*),证明:数列{bn}为等比数列;
(2)设cn= (n∈N*),证明:数列{cn}为等差数列;
(n∈N*),证明:数列{cn}为等差数列;
(3)求Sn=a1+a2+…+an。
(1)设bn=an+1-2an(n∈N*),证明:数列{bn}为等比数列;
(2)设cn=
 (n∈N*),证明:数列{cn}为等差数列;
(n∈N*),证明:数列{cn}为等差数列;(3)求Sn=a1+a2+…+an。
解:(1)由Sn+1=4an+2,得an+1=Sn+1-Sn=(4an+2)-(4an-1+2)(n≥2)
∴an+1-2an=2an-4an-1=2(an-2an-1)
故数列{an+1-2an} 是以a2-2a1为首项,2为公比的等比数列,又a1=1,a1+a2=S2=4a1+2,
所以a2=5
∴bn=an+1-2an=3·2n-1;
(2)将an+1-2an=3·2n-1两边同除以2n+1,则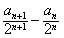
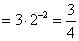 ,即
,即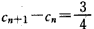
故{cn}是以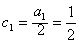 为首项,
为首项,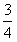 为公差的等差数列;
为公差的等差数列;
(3)由(2)知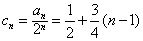 ,得an=(3n-1)·2n-2
,得an=(3n-1)·2n-2
又Sn=4an-1+2,则Sn=4(3n-4)·2n-3+2=(3n-4)·2n-1+2。
∴an+1-2an=2an-4an-1=2(an-2an-1)
故数列{an+1-2an} 是以a2-2a1为首项,2为公比的等比数列,又a1=1,a1+a2=S2=4a1+2,
所以a2=5
∴bn=an+1-2an=3·2n-1;
(2)将an+1-2an=3·2n-1两边同除以2n+1,则
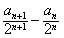
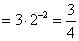 ,即
,即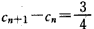
故{cn}是以
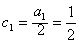 为首项,
为首项,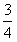 为公差的等差数列;
为公差的等差数列;(3)由(2)知
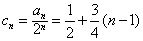 ,得an=(3n-1)·2n-2
,得an=(3n-1)·2n-2又Sn=4an-1+2,则Sn=4(3n-4)·2n-3+2=(3n-4)·2n-1+2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
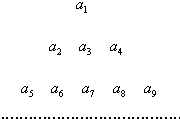 已知数列{an}中,an=n(n∈N+),把它的各项依次排列如图所示的三角形状,第一行1项,第二行3项,…第一行 a1
已知数列{an}中,an=n(n∈N+),把它的各项依次排列如图所示的三角形状,第一行1项,第二行3项,…第一行 a1