题目内容

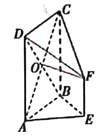
【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，E为DD1中点.

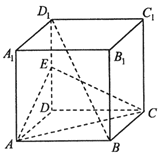
（1）求证：BD1∥平面ACE；

（2）求证：BD1⊥AC.

【答案】（1）见解析；（2）见解析

【解析】

（1）设AC与BD交于点O，连接OE，根据菱形的性质和三角形的中位线定理可得OE∥D1B，再由线面平行的判定定理可得证；

（2）由菱形的性质可得AC⊥BD，再由线面垂直的性质得DD1⊥AC，根据线面垂直的判定和性质可得证.

（1）设AC与BD交于点O，连接OE，∵底面ABCD是菱形，∴O为DB中点，又因为E是DD1的中点，∴OE∥D1B，

∵OE面AEC，BD1平面AEC，∴BD1∥平面ACE.

（2）∵底面ABCD是菱形，∴AC⊥BD，∵DD1⊥底面ABCD，∴DD1⊥AC，且DB∩DD1＝D，

∴AC⊥平面BDB1D1.∵BD1平面BDD1B1，∴AC⊥BD1.

练习册系列答案
相关题目

【题目】(1)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:

排队人数

0

1

2

3

4

5人及5人以上

概率

求至少3人排队等候的概率是多少?

(2)在区间上随机取两个数m,n,求关于x的一元二次方程有实根的概率.

【题目】已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1,y=f(x)在x=-2处有极值．

(1)求f(x)的解析式．

(2)求y=f(x)在[-3,1]上的最大值．

【题目】如图，在五面体中，侧面是正方形，是等腰直角三角形，点是正方形对角线的交点，且.

（1）证明：平面；

（2）若侧面与底面垂直，求五面体的体积.

【题目】若数列、满足 (N*)，则称为数列的“偏差数列”.

（1）若为常数列，且为的“偏差数列”，试判断是否一定为等差数列，并说明理由；

（2）若无穷数列是各项均为正整数的等比数列，且，为数列的“偏差数列”，求的值；

（3）设，为数列的“偏差数列”，，且，若对任意恒成立，求实数M的最小值.

【题目】如图,在四棱锥中,底面是菱形,点在线段PC上,且三棱锥的体积是四棱锥的体积的,,平面.

（1）若是的中点,证明:直线∥平面;

（2）求二面角的正弦值.

【题目】在平面直角坐标系中，以为极点，轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为，直线的参数方程为为参数，直线与曲线分别交于两点.

（1）若点的极坐标为，求的值；

（2）求曲线的内接矩形周长的最大值.

【题目】如图，在直三棱柱ABC-A1B1C1中，点M，N分别为线段A1B，B1C的中点．

（1）求证：MN∥平面AA1C1C；

（2）若∠ABC=90°，AB=BC=2，AA1=3，求点B1到面A1BC的距离．

【题目】某年级100名学生期中考试数学成绩（单位:分）的频率分布直方图如图所示，其中成绩分组区间是[50，60)，[60，70)，[70，80)，[80，90)，[90，100].

（1）求图中a的值，并根据频率分布直方图估计这100名学生数学成绩的平均分；

（2）从[70，80)和[80，90)分数段内采用分层抽样的方法抽取5名学生，求在这两个分数段各抽取的人数；

（3）现从第（2）问中抽取的5名同学中任选2名参加某项公益活动，求选出的两名同学均来自[70，80)分数段内的概率.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网