题目内容
以初速度40 ,垂直向上抛一物体,
,垂直向上抛一物体,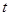 时刻的速度(
时刻的速度(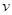 的单位是
的单位是 )为
)为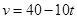 ,则该物体达到最大高度为 .米
,则该物体达到最大高度为 .米
 ,垂直向上抛一物体,
,垂直向上抛一物体,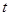 时刻的速度(
时刻的速度(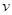 的单位是
的单位是 )为
)为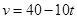 ,则该物体达到最大高度为 .米
,则该物体达到最大高度为 .米80
先求物体达到最大高度即其速度为0时,物体运动时间,再将物体最大高度问题转化为速度函数在时间上的定积分问题,利用微积分基本定理计算定积分的值即得最大高度
解:令v=0,得t=4
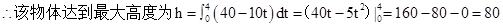
故答案为 80

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
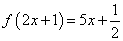 ,那么
,那么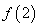 的值是 ( )
的值是 ( ) 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围( )
的取值范围( )



 与
与 的定义域是
的定义域是
 ,函数
,函数 ,则
,则



 ,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件. .P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率
.P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率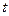 的最大值.
的最大值.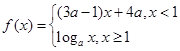 满足:对任意实数
满足:对任意实数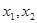 ,当
,当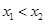 时,总有
时,总有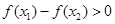 ,那么实数
,那么实数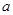 的取值范围是 ( )
的取值范围是 ( )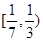
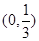
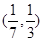
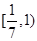
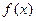 ,(
,(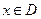 ),若同时满足以下条件:
),若同时满足以下条件: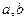 ]
]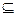 D,使
D,使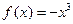 符合条件②的区间[
符合条件②的区间[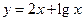 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[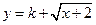 是闭函数,求实数
是闭函数,求实数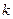 的取值范围.
的取值范围.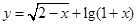 的定义域为( )
的定义域为( )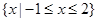
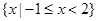
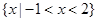
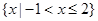
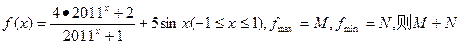 =
=